Verification Example

We now consider an example to illustrate how the model checker works. We consider the simplified Needham-Schroeder protocol analyzed by Lowe [16] given below:

1.

$A \rightarrow B : A.B.\{ N_{a}.A \}_{K_{B}}$

2.

$B \rightarrow A : B.A.\{ N_{a}.N_{b} \}_{K_{A}}$

3.

$A \rightarrow B : A.B.\{ N_{b} \}_{K_{B}}$

Here A is the initiator and B is the responder. A selects a nonce $N_{a}$ and sends it along with its name encrypted with B 's public key to B . B uses its private key to decrypt this message and obtain $N_{a}$. Now B generates its own nonce $N_{b}$ and sends it along with $N_{a}$ encrypted with A 's public key to A . A uses its private key to decrypt this message and returns $N_{b}$ to B encrypted with B 's public key. B then uses its private key to verify that it has just received the nonce sent earlier.

In order to use our model checker, we first isolate which actions are performed by A and which actions are performed by B . We then write a short sequence of actions which make up each participant's role in the protocol. The process description for principal A can be found in figure 4. The description for principal B is similar. All that remains is to specify the initial state of each principal's local store. Each principal, including the intruder, knows the names of all three principals. Each principal also knows the public key of each of the three principals. Finally, each principal knows it's own private key. Figure 5 lists the initial contents of the intruder's local store which consists of the names of the three principals, all three public keys and it's own private key.

   Figure 4: Process description for the initiator

((beginit (*p-var* b))
 (newnonce (*var* na))
 (send (*var* b)
       (concat a
               (*var* b)
               (encrypt (pubkey (*var* b)) (concat (*var* na) a))))
 (receive (*var* b)
          (concat (*var* b)
                  a
                  (encrypt (pubkey a) (concat (*var* na) (*var* nb)))))
 (send (*var* b)
       (concat a
               (*var* b)
               (encrypt (pubkey (*var* b)) (*var* nb))))
 (endinit (*var* b)))

   Figure 5: The intruder's initial knowledge

The result of the verification attempt can be found in figure 6. In just a few seconds, the model checker finds a violation of the security specification and generates a counter-example. Figure 7 provides an easier to read description of the attack. The sequence of messages for two runs of the protocol $(\alpha \mbox{ and } \beta)$ are provided. The notation I(A) is meant to convey either I impersonating A if on the left of the arrow, or I intercepting a message meant for A if on the right of the arrow.

If we examine the counter-example we can see what has happened. A initiates a protocol run with the intruder. The intruder initiates a protocol run with B impersonating A and using the same nonce that A used with the intruder. When B responds, the intruder forwards this message to A . This message has the format that A is expecting, namely its own nonce and a new nonce encrypted with A 's public key. A then replies back to the intruder with B 's nonce encrypted with the intruder's public key. The intruder can use its private key to decrypt this and it can now return B 's nonce encrypted with B 's public key. When B receives this message, the protocol run is complete and B believes it has finished a protocol run with A while A does not have the corresponding belief that it has initiated a protocol run with B .

The above analysis is most easily seen in figure 7 by observing the following relationship between the $\alpha$ run and the $\beta$ run:

• The role of A in $\alpha$ is played by I in $\beta$.
• The role of I in $\alpha$ is played by B in $\beta$.
• Each message in $\beta$ can be obtained from the corresponding message in $\alpha$ by replacing every occurance of I with B .

Therefore, the $\beta$ run is identical to the $\alpha$ run except that B plays the role of the responder and I impersonating A has played the role of the initiator.

   Figure 6: Verification Result

"Lack of correspondence" 
(B (BEGRESPOND A)) 
(A (BEGINIT *INTRUDER*)) 
(A ((NEWNONCE (*VAR* NA)) (*NONCE* 245))) 
(A
 (CONCAT A *INTRUDER*
  (ENCRYPT (PUBKEY *INTRUDER*) (CONCAT (*NONCE* 245) A)))
 INTRUDER) 
(INTRUDER (CONCAT A B (ENCRYPT (PUBKEY B) (CONCAT (*NONCE* 245) A))) B) 
(B ((NEWNONCE (*VAR* NB)) (*NONCE* 260))) 
(B
 (CONCAT B A (ENCRYPT (PUBKEY A) (CONCAT (*NONCE* 245) (*NONCE* 260))))
 INTRUDER) 
(INTRUDER
 (CONCAT *INTRUDER* A
  (ENCRYPT (PUBKEY A) (CONCAT (*NONCE* 245) (*NONCE* 260))))
 A) 
(A (CONCAT A *INTRUDER* (ENCRYPT (PUBKEY *INTRUDER*) (*NONCE* 260)))
 INTRUDER) 
(A (ENDINIT *INTRUDER*)) 
(INTRUDER (CONCAT A B (ENCRYPT (PUBKEY B) (*NONCE* 260))) B)

   Figure 7: Attack on Needham-Schroeder Protocol

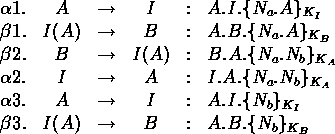
Lowe suggests fixing the protocol by changing the second message so that the new protocol is as follows:

1.

$A \rightarrow B : A.B.\{ N_{a}.A \}_{K_{B}}$

2.

$B \rightarrow A : B.A.\{ N_{a}.N_{b}.B \}_{K_{A}}$

3.

$A \rightarrow B : A.B.\{ N_{b} \}_{K_{B}}$

When we try to verify this protocol, like Lowe, we find no attack in a single run of the protocol. Because no attack was found, the entire exhaustive search of the state space is performed and so the verification process takes a bit longer, but it still completed in under a minute.