Information Algorithms

While Corollary 3 proves the decidability of determining if $x \in \overline{B}$, it is an extremely inefficient algorithm. In particular, enumerating all sequences of expanding rules of length $\mu(x)$ will yield exponential complexity. In practice however, we can search for a derivation of x from $B_{s}$ by using the structure of x . Specifically, we have the following theorems:

Theorem 4: $m_{1} \cdot m_{2} \in \overline{B_{s}}$ if and only if $m_{1} \cdot m_{2} \in B_{s}$ or $m_{1} \in \overline{B_{s}}$ and $m_{2} \in \overline{B_{s}}$.

Proof: Assume $m_{1} \cdot m_{2} \in \overline{B_{s}}$ and $m_{1} \cdot m_{2} \not\in {B_{s}}$, then $m_{1} \cdot m_{2}$ must be in $\overline{B_{s}}$ because of an expanding rule. By assumption, $m_{1} \cdot m_{2} \not\in {B_{s}}$. To show that $m_{1} \cdot m_{2} \in \overline{B_{s}}$ can be derived from $B_{s}$ without using a shrinking rule we take a derivation of $m_{1} \cdot m_{2} \in \overline{B_{s}}$,$\Gamma$, and use theorem 2 to get a normalized derivation $\Gamma'$.Now either the shrinking rules appearing in $\Gamma'$ are redundant (i.e. they don't add any new words and so can be removed from the derivation) or we contradict the fact that $B_{s}$ was created by applying all possible shrinking rules to B . In either case the remainder of the derivation (and there must be some remainder since we assume that $m_{1} \cdot m_{2} \not\in {B_{s}}$) must consist of expanding rules. In particular the last rule used in the derivation must be an expanding rule and the only way that could be the case is if it is rule 2 which would require as its premise $m_{1} \in \overline{B_{s}}$ and $m_{2} \in \overline{B_{s}}$.

Now assume that $m_{1} \cdot m_{2} \in B_{s}$ or $m_{1} \in \overline{B_{s}}$ and $m_{2} \in \overline{B_{s}}$. Then it is clear by either rule 1 or rule 2 that $m_{1} \cdot m_{2} \in \overline{B_{s}}$.

Theorem 5: $\{ m \}_{k} \in \overline{B_{s}}$ if and only if $\{ m \}_{k} \in B_{s}$ or $m \in \overline{B_{s}}$ and $k \in \overline{B_{s}}$.

Proof: Analogous to the previous theorem.

Putting all these together yields the basis for our search algorithm. As our set of known messages increases, we repeatedly apply shrinking rules and removing ``redundant messages'' until we get a set of ``basic'' messages, $B_{s}$, to which we cannot apply any shrinking rules. By redundant messages, we mean messages that can be generated from the other messages in the set using expanding rules. For example, when we apply rule 3 to get $m_{1}$ and $m_{2}$ from $m_{1} \cdot m_{2}$, we also remove $m_{1} \cdot m_{2}$ from $B_{s}$.However, when applying rule 5 we must be careful; when we generate m from $\{ m \}_{k}$ and $k^{-1}$ we cannot remove $\{ m \}_{k}$ from $B_{s}$ unless $k \in B_{s}$. Pseudocode for this algorithm is given in figure 2.

   Figure 2: Augmenting the intruder's knowledge

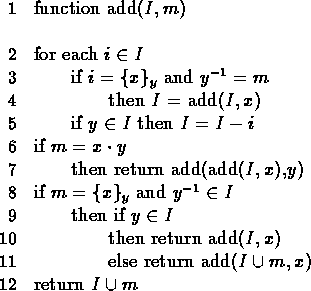
We now consider the complexity of inserting a new message m into our current set of information $B_{s}$ and generate a new set of information $B'_{s}$. The only time there is any interaction between previously known messages in $B_{s}$ and m is when we try to apply the decryption rule. The message m can have at most |m| encryptions. For each encryption, we scan $B_{s}$ looking for the inverse key for a total of $\vert B_{s}\vert\vert m\vert$ time. Analogously, m could contain at most |m| keys. For each key, we must check each element of $B_{s}$ to see if it can now be decrypted. Again, this takes at most $\vert B_{s}\vert\vert m\vert$ time. However, the newly decrypted message could again be decrypted. The number of iterations is bounded by $\vert B_{s}\vert$;therefore, the total time to generate $B'_{s}$, is bounded by $O(\vert B_{s}\vert^{2}\vert m\vert)$ and the size of $B'_{s}$ is bounded by $O(\vert B_{s}\vert^{2})$.

We know that any words in $\overline{B_{s}}$ can be derived using only expanding rules. When we search to see if a word w is known, we can use theorems 4 and 5 to break it down into smaller pieces which can then be searched recursively. For example, if $w \not\in B_{s} \mbox{ and } w = \{ m \}_{k}$, then theorem 5 tells us that $w \in \overline{B_{s}}$ only if $m \in \overline{B_{s}} \mbox{ and } k \in \overline{B_{s}}$.Pseudocode for this algorithm is given in figure 3.

   Figure 3: Searching the intruder's knowledge

When searching for a derivation of w from $B_{s}$ we first check to see if $w \in B_{s}$. This costs at most $\vert B_{s}\vert$ time. If not, we break down w into two smaller pieces and recursively check those peices. The total number of recursive calls is bounded by the number of operations making up w , which is in turn bounded by |w| . Thus the total time to check if $w \in \overline{B_{s}}$ is bounded by $O(\vert B_{s}\vert\vert w\vert)$.