Verification

In this section, we show how to combine roles and inference rules so as to perform the verification of a given cryptographic authentication protocol. To keep the presentation simple, we will confine ourselves to the analysis of authentication properties. We will show further how to easily extend our verification algorithm to deal with security properties.

A principal A wishing to prove his identity to a principal B , has to answer all the challenges uttered by B . Hence, the intruder can impersonate the principal A if he can answer all those challenges uttered by B to A . Thus, the verification principal consists in checking whether the intruder, with all its computation abilities, can answer such challenges.

Actually, the intruder computation abilities consist of:

• An initial knowledge generally made of the keys that the intruder shares with other principals, the server identity and other principal identities. Notice that this initial knowledge must be given explicitly within the protocol specification.
• The usual encryption, decryption, composition and decomposition abilities. Indeed, the intruder could encrypt and decrypt any message under known keys. In addition, he has the ability to compose (catenate) and decompose messages.
• Those computation abilities given by the protocol itself and captured by the deductive proof system.

Now we come to the explanation of the verification procedure. Starting from the protocol description, we extract the roles. Now, for each role, the intruder will attempt to answer all the challenges uttered so as to perform a masquerade. The intruder will progressively follow the role in a stepwise way. For a given step, if the role sends a message, the intruder will merely store it and hence will extend his knowledge. If the role is waiting for receiving some particular message, the intruder will attempt to generate it using his current computation abilities. In other words, the intruder will try to synthesize the required message using his current knowledge modulo some composition/decomposition and encryption/decryption steps, and also up to the use of the deductive proof system.

Now, let us see how this applies to the unidirectional Woo and Lam authentication protocol of Table 1. Notice that the only concerned role is B . The corresponding role is:

$$\begin{array} {lcl} Role(B) & = & \mbox{$\langle {?, A, A} ... ...ox{$\langle {?, \{ N_b \}_{k_{bs}} , S} \rangle$} \end{array}$$

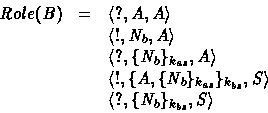
Actually, before starting to take up the various challenges uttered by B , we have first to proceed to what we call the generalization of the role B . This operation aims to replace some messages by message variables as done in the deductive proof system. The rationale underlying such substitutions is that these messages could not be verified from the content, structure, freshness and type standpoint. This operation will be formally defined in the next section. The role B is rewritten into:

$$\begin{array} {lcl} Role(B) & = & \mbox{$\langle {?, A, A} ... ...ox{$\langle {?, \{ N_b \}_{k_{bs}} , S} \rangle$} \end{array}$$

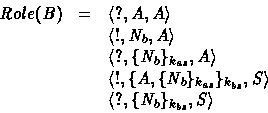
Here, we replace the message $\{N_b\}_{k_{as}}$ by a message variable X since B does not know the key $k_{as}$, hence he could accept any other information.

First of all, let us initialize the knowledge of the intruder, noted KI , with the intruder initial knowledge. In other words, KI is set to $\{k_{is},A,B,S\}$. This means that the intruder initially knows the identity of the server S , his shared key with S , the role A and the role B .

Now the verification amounts to a constraint satisfaction problem. In fact, we are going to collect constraints that reflect the requirements that makes the intruder take up successfully all the challenges uttered by a particular role.

In the first step of the role B , the principal is waiting for a message identifier, say A . To take up this challenge, the intruder has to generate such an identifier from KI modulo some composition/decomposition and encryption/decryption steps, and also up to the use of the deductive proof system. Such a constraint is written as:

$(E_1)$ $KI \models_R A$

where R stands for the set of the rules $R_1,\ldots, R_5$ of Table 3 together with the usual composition/decomposition and encryption/decryption rules.

At the second step, B sends the nonce $N_b$ over the network. Hence, the message becomes available to the intruder who extends his current knowledge to become $K_2 = KI \cup \{N_b\}=\{k_{is},A,B,S, N_b\}$.

At the third step, the intruder must supply B with X . Notice that the current knowledge of the intruder at this step is $K_2$. Accordingly, this second constraint will be written as:

$(E_2)$ $KI\cup\{N_b\}\models_R X$

At the fourth step, B offers the message $\{ A, X \}_{k_{bs}}$ to the intruder. The latter updates his knowledge to become $KI\cup\{N_b, \{ A,X\}_{k_{bs}}\}$.

Finally, the intruder has to supply the role B with $\{N_b\}_{k_{bs}}$ in order to achieve the masquerade. This last constraint will be written as:

$(E_3)$ $KI\cup\{N_b, \{ A,X\}_{k_{bs}}\} \models_R \{ N_b \}_{k_{bs}}$

At this level, we are ready to check whether the intruder can or cannot impersonate the role A . This amounts to check the existence of solutions to the constraint set $\{ E_1,E_2,E_3 \}$ which is the following system:

$$\left \{ \begin{array} {lcl} \{k_{is},A,B,S,I\} & \models_... ...{bs}}\}& \models_R &\{ N_b \}_{k_{bs}} \end{array} \right \}$$

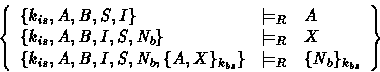
In fact, we use the resolution as a decision procedure for the simultaneous resolution of these constraints. The decision procedure yields a set of substitutions each of which denotes a potential flaw. Furthermore, the inference rules of the proof system are annotated by the associated scenarios. Thus, the application of these inference rules propagates these scenarios. Such a propagation yields also complete attack scenarios. To sum up, we extract automatically flaws and attack scenarios from protocol specifications.

In the case of the constraint set $\{ E_1,E_2,E_3 \}$, the algorithm produces many flaws and attack scenarios. Most of these attacks are new and completely different from those known up to now. In what follows, we present in Table 4 one among the many elegant attacks yielded by our algorithm.

  Table 4:   An Attack of the Woo and Lam Authentication Protocol

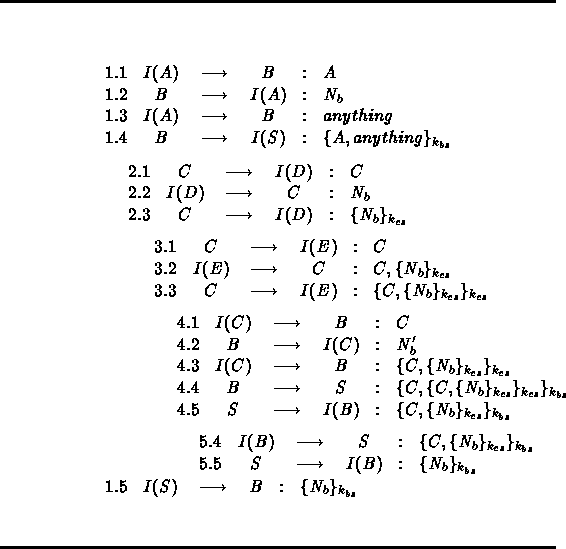
The reader should notice that the attack reported in Table 4 is both elegant and sophisticated. The elegance of the attack stems from three facts:

1.

First, the attack involves five sessions, hence we believe that the attack cannot be generated manually (at least in an easy way).

2.

Second, notice that the intruder does not make any use of his key. Consequently, the intruder can be an illegal user of the system.

3.

Third, the intruder impersonates A without opening any protocol session with the principal A . Hence, A could be not operational when the intruder performs the attack.

Here is the way the attack of Table 4 could be carried out: In the communication step ``1.1.'', the intruder begins a session with B in order to claim that his identity is A . In the step ``1.2.'', the intruder I intercepts the nonce $N_b$ generated by B and send it to A . In the step ``1.3.'', I replies by a message anything which means any message since B cannot do any verification. In the step ``1.4.'', B must react according to the protocol by sending the message $\{A,anything\}_{k_{bs}}$. This message will be intercepted by the intruder. To finish this protocol run, the intruder ultimately needs to synthesize the message $\{N_b\}_{k_{bs}}$ in order to send it to B at the step ``1.5.''. To get this last required message, the intruder will open the sessions 2, 3 and 4. Notice that such a message could be get in a simpler way but for the sake of elegance we use all these sessions.

At the session 2, the intruder I waits for a principal C to initiate a session with another principal D . Then, he intercepts the message C and replies by the nonce $N_b$ in order to get the message $\{N_b\}_{k_{cs}}$ at the step 3 of this session. This message will be used to generate the message $\{C,\{N_b\}_{k_{cs}}\}_{k_{cs}}$. Indeed, the intruder has to wait that the same principal C initiates another session with another principal E as shown in Table 4. At the session 4, the intruder wants to obtain the message $\{C,\{N_b\}_{k_{cs}}\}_{k_{bs}}$ which makes easy getting the message $\{N_b\}_{k_{bs}}$. For instance, the intruder replies by the message $\{C,\{N_b\}_{k_{cs}}\}_{k_{cs}}$ as the C 's answer which is supposed to be $\{N'_b\}_{k_{cs}}$. At the session 5, the intruder gets easily the message $\{N_b\}_{k_{bs}}$ by sending the message obtained at the session 4 to the server S .

Finally, the intruder terminates the first session, step ``1.5.'', with B , by sending the message $\{N_b\}_{k_{bs}}$ as an S 's response. Hence, from now on B is convinced that the initiator of the session one is A .