Proof System Generation

In cryptographic protocol design, we always assume the presence of an intruder that has a complete control over the communication network. Accordingly, the intruder is able to intercept, modify, store, retrieve and send any circulating message in the network. Moreover, we assume that the intruder has the usual encryption and decryption abilities. In this work, we consider another valuable source of information available to the intruder: the protocol itself. Actually, the protocol may be viewed by the intruder as a computation engine which may be used to synthesize and deliver some particular information that makes possible a fatal attack.

In our approach, we capture all these intruder abilities by a deductive proof system. We associate to each protocol step an inference rule. Each inference rule captures one possible instrumentation of the protocol. The general form of an inference rule is:

$$\mbox{$\frac{\displaystyle {\mbox{$p_1\ldots p_n$}}}{\displaystyle {m} } $} ~c$$

where $p_1,\ldots ,p_n,m$ are messages and c is a boolean formula. This inference rule should be read as follows: the intruder could supply the protocol with the messages $p1,\ldots ,p_n$ and get the message m from the protocol provided that the side condition c holds. In fact, the side condition refers to those freshness conditions dictated by the protocol. Furthermore, we will endow each inference rule with a sequence of protocol steps (a scenario) showing how the intruder could instrument the protocol with the information $p_1,\ldots , p_n$ so as to get the message m .

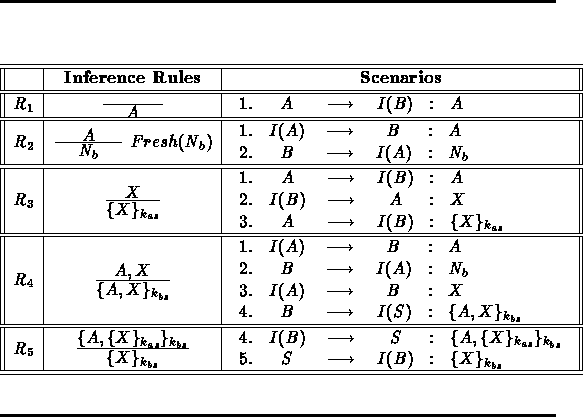
Now, let us see how this applies to the Woo and Lam protocol of Table 1. For the sake of clarity, we present here the inference rules together with the associated scenarios without explaining how they are generated. Such explanations will be given further in the sequel.

The first step in the Woo and Lam protocol of Table 1 is:

$${\rm 1.}\;\;A\longrightarrow B: A$$

The inference rule associated with this protocol step is:

$$\mbox{$\frac{\displaystyle {\ \ \ \ \ \ \ }}{\displaystyle {A} } $}$$

meaning that the intruder could get from the protocol the identity of any principal wishing to initiate a protocol session. Here is the scenario that makes this possible:

$${\rm 1.}\;\;A\longrightarrow I(B): A$$

This sequence stipulates that the intruder could get the identity of a principal A by intercepting the message sent by this principal when wishing to initiate a new protocol session. In doing so, the intruder I performs a masquerade on the role of a principal B, which is written I(B) . Later in this section, we will present inference rules that capture sophisticated computations.

The second step in the Woo and Lam protocol of Table 1 is:

$${\rm 2.}\;\;B\longrightarrow A: N_b$$

The inference rule associated with this protocol step is:

$$\mbox{$\frac{\displaystyle {\ \ A \ \ }}{\displaystyle {N_b} } $} ~ Fresh(N_b)$$

meaning that the intruder could get a fresh nonce (generated by B ) from the protocol just by supplying it with an agent identity. The side condition $Fresh(N_b)$ stipulates the freshness of the information $N_b$. Here is the scenario that illustrates such a situation:

$$\begin{array} {llclcl} {\rm 1.} & I(A) & \longrightarrow & ... ...\ {\rm 2.} & B & \longrightarrow & I(A) &:& N_b \end{array}$$

This sequence stipulates that the intruder does a masquerade on the role A . First, the intruder sends to B the principal identifier A . According to the protocol, the principal B will react by generating a fresh nonce $N_b$ and sending it on the network to A , hence to I(A) .

The third step in the Woo and Lam protocol of Table 1 is:

$${\rm 3.}\;\;A\longrightarrow B: \{ N_b \}_{k_{as}}$$

The inference rule associated with this protocol step is:

$$\mbox{$\frac{\displaystyle {\ \ X \ \ }}{\displaystyle { \{ X \}_{k_{as}} } } $}$$

meaning that the intruder could supply the protocol with any information X and get it encrypted under the secret key shared between the server S and a principal A . At this level, we would like to pinpoint one important feature in our verification algorithm. The reader should notice that we used X in the inference rule instead of $N_b$. The rationale underlying this choice is that the principal A , at the third step of the protocol, replies with the message received at the second step (i.e. $N_b$) encrypted by $k_{as}$. Notice that $N_b$ is a nonce generated and uttered by B and sent to A . Now, let us mention the following facts:

• The principal A has no preliminary knowledge on the effective value of the expected message at the second step of the protocol. Accordingly, A has no means to verify the value of the received message at that step.
• The freshness of $N_b$ is a local property. In other words, the freshness of the nonce cannot be attested by any principal other than B . So, A cannot require the freshness of the message received at the second step of the protocol.
• For the sake of generality, we assume that the exchanged messages are not typed. Consequently, A is unable to verify the type of the message received at the second step of the protocol.

Owing to these three facts, A can verify neither the value, the freshness nor the type of the message received at the second step of the protocol. Consequently, A will accept any message at that step and will reply by sending the encrypted version of this message under the key $k_{as}$. This explains the rationale underlying the use of a variable message X instead of $N_b$. We will show further how fatal attacks could stem from this second protocol step.

Here is the scenario that exhibits how the intruder could instrument the protocol so as to get the message $\{ X \}_{k_{as}}$ provided that he supplies the protocol with X :

$$\begin{array} {llclcl} {\rm 1.} & A & \longrightarrow & I(B... ... & A & \longrightarrow & I(B) &:& \{X\}_{k_{as}} \end{array}$$

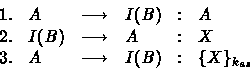
This sequence stipulates that the intruder will do a masquerade on the role B . First, the intruder will wait for A to initiate a protocol session i.e. to send the message A which will be intercepted by I(B) . Next, the intruder I(B) will send a message X to the principal A . The latter will react innocently by sending the message $\{ X \}_{k_{as}}$.

From now on, it is clear that the intruder has the ability to encrypt any known message X with the secret key $k_{as}$ shared by the server and a principal A . Indeed, this ability follows from the three-steps sequence above. This highlights a weakness in the design of the Woo and Lam protocol. More dramatically, the intruder could encrypt any known message X by any shared key $k_{ps}$ where p stands for any principal identifier. The reader should notice that in the protocol specification the principal identifier A is implicitly universally quantified over all principals.

Now, let us give some general comments regarding the inference rules and the associated scenarios. First, the agent identifiers as well as the introduced variables are implicitly universally quantified. Second, the generated scenarios constitute proofs of the correction of the inference rules. Actually, the scenarios are propagated during the deduction process.

The fourth step in the Woo and Lam protocol of Table 1 is:

$${\rm 4.}\;\;B\longrightarrow S: \{ A, \{ N_b \}_{k_{as}} \}_{k_{bs}}$$

The inference rule associated with this protocol step is:

$$\mbox{$\frac{\displaystyle {\ \ A \ \ X \ \ }}{\displaystyle { \{ A, X \}_{k_{bs}} } } $} ~$$

meaning that the intruder could supply the protocol with a principal identifier, say A , and a known message X so as to get an encrypted version of the composition of these two messages under the key $k_{bs}$. Here is the scenario that illustrates such a situation:

$$\begin{array} {llclcl} {\rm 1.} & I(A) & \longrightarrow & ... ...& \longrightarrow & I(S) &:& \{ A, X \}_{k_{bs}} \end{array}$$

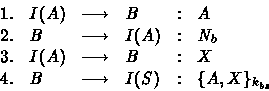
This sequence stipulates that the intruder will do a masquerade on the role A . First, the intruder sends to B the principal identifier A . According to the protocol, the principal B reacts by generating a fresh nonce $N_b$ and sending it on the network to A , hence to I(A) . The next step is very sensible from the security standpoint. In fact, at the third step, the principal B is waiting for a message ($N_b$) encrypted under a key ($k_{as}$) that is locally unknown (from B standpoint). Nevertheless, the principal B has no means to check neither that the received message at the third step is effectively encrypted under $k_{as}$ ($k_{as}$ is unknown to B ), nor that its content is $N_b$. Hence, the principal B can accept any message, say X , at this third step. Finally, the principal B reacts confidently with the message $\{ A, X \}_{k_{bs}}$. This pinpoints a second weakness in the design of the Woo and Lam protocol.

The fifth step in the Woo and Lam protocol of Table 1 is:

$${\rm 5.}\;\;S\longrightarrow B: \{ N_b \}_{k_{bs}}$$

The inference rule associated with this protocol step is:

$$\mbox{$\frac{\displaystyle { \ \ \{ A, \{ X \}_{k_{as}} \}_{k_{bs}} \ \ }}{\displaystyle { \{ X \}_{k_{bs}} } } $}$$

meaning that the intruder could supply the protocol with a message of the form $\{ A, \{ X \}_{k_{as}} \}_{k_{bs}}$ so as to get the message $\{ X \}_{k_{bs}}$. Here is the scenario that illustrates such a situation:

$$\begin{array} {llclcl} {\rm 4.} & I(B) & \longrightarrow & ... ... S & \longrightarrow & I(B) &:& \{ X \}_{k_{bs}} \end{array}$$

This sequence stipulates that the intruder will do a masquerade on the role B . First, the intruder sends to the server the message $\{ A, \{ X \}_{k_{as}} \}_{k_{bs}}$. According to the protocol, the server decrypts such a message twice (using $k_{bs}$ then $k_{as}$) and sends the sub-message X encrypted under the key $k_{bs}$. Notice that the server, at the fourth step, is normally expecting a message of the form $\{ A, \{N_b\}_{k_{as}} \}_{k_{bs}}$. However, the server can check neither the value, the freshness nor the type of $N_b$. Accordingly, the server accepts any other information instead of $N_b$. This explains the rationale underlying the use of X instead of $N_b$ in the previous inference rule.

From now on, it is clear that the intruder has extra decrypting abilities. In addition to the usual ones, the intruder can instrument the protocol to decrypt messages encrypted under keys that are unknown to him. For instance, assume that the intruder is wishing to decrypt a message of the form $\{ X \}_{k_{as}}$. Recall also that the intruder may be a legal principal that shares a symmetric key $k_{is}$ with the server. The intruder can merely supply the server with the message $\{ A,\{X\}_{k_{as}}\}_{k_{is}}$ to get finally the message $\{ X \}_{k_{is}}$ which he can decrypt to extract X . Here, the intruder has used the server as an oracle to decrypt messages. Notice that this example illustrates only one possible application (among many) of the previous inference rule. This pinpoints a third weakness in the design of the Woo and Lam protocol.

We sum up in Table 3 the whole proof system that has been generated from the Woo and Lam protocol of Table 1. The inference rules and the associated scenarios have been automatically generated from the protocol specification. The generation method will be explained further in the sequel.

  Table 3:   The Deductive Proof System Associated with the Woo and Lam Protocol