Comparison with BAN logic

Next: Rectification of formulas Up: The logic Previous: Axiomatisation

Comparison with BAN logic

In order to understand the relation between our logic and BAN logic, we show that every theorem of BAN logic is a theorem of our logic -- in other words, that our logic is stronger. Because our logic stripped off the $\believes$ operator from most of the axioms, the following lemma will be useful in the proof.

$\begin{lemma} If \ $\derives \phiimplpsi$, then \ $\derives P \believes \phi \implies P \believes \psi$.\end{lemma}$

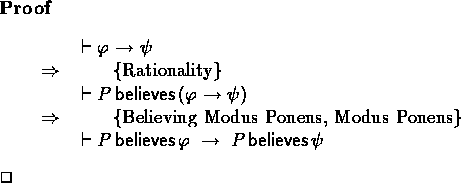
$\begin{proof} \begin{calc} \xpr{\derives \phiimplpsi} \z{\Rightarrow}{Rationalit... ...} \xpr{\derives P \believes \phi \implies P \believes \psi}\end{calc}\end{proof}$

From Believing Modus Ponens and the Rationality Rule we now obtain:

$\begin{lemma} $ \derives P \believes (\phi \:\land\: \psi) \;\iff\; P \believes \phi \:\land\: P \believes \psi $\end{lemma}$

If part of a message is fresh, the whole of the message must be fresh as well:
$\begin{lemma} $ \derives \fresh X \implies \fresh(X,Y) $\end{lemma}$
Note that the reverse does not hold, since a message can contain ``old news'' next to new data; the combination is fresh, but every element is not.

$\begin{theorem} The logic as defined in this article, is stronger than BAN logic.\end{theorem}$

Proof

It suffices to prove that all axioms of the BAN logic are theorems of our logic.

$\banderives P \sees (X,Y) \implies P \sees X$

is our axiom Seeing parts of a joint message, and therefore a theorem.

$\banderives P \believes \phi \:\land\: P \believes \psi \implies P \believes (\phi,\psi)$

$\banderives P \believes (\phi,\psi) \implies P \believes \phi$

both follow from Lemma 4 using the identification of the joining operator on formulas with the logical-and operator.

$\banderives P \believes \key{Q}{R}{K} \implies P \believes \key{R}{Q}{K}$

follows from the symmetry of the $\barekey$ operator.

$\banderives P \believes Q \oncesaid (X,Y) \implies P \believes Q \oncesaid X$

follows from our axiom Saying parts of a joint message and Lemma 3.

$\banderives P \believes \key{P}{Q}{K} \:\land\: P \sees \encrypt{X}{K}{Q} \implies P \sees X$

follows from our axioms Possessing believed keys and Decryption.

$\banderives P \believes \key{P}{Q}{K} \:\land\: P \sees \encrypt{X}{K}{Q} \implies P \believes Q \oncesaid X$

follows from our axiom Awareness and Lemmas 3 and 4.

$\banderives P \believes \fresh \phi \:\land\: P \believes Q \oncesaid \phi \implies P \believes Q \believes \phi$

follows from the definition of $\fresh$ ,the idempotence of $\concate$ ,and Lemmas 3 and 4.

$\banderives P \believes \fresh X \implies P \believes \fresh(X,Y)$

follows from Lemmas 3 and 5.

$\banderives P \believes Q \controls \phi \:\land\: P \believes Q \believes \phi \implies P \believes \phi$

follows from the definitions of $\controls$ and $\rightlybelieves$ and Lemmas 3 and 4.

$\fbox {\vphantom{\tiny .}}$

Next: Rectification of formulas Up: The logic Previous: Axiomatisation