Rectification of formulas

The rectify operation $\rectify{\placeh}$ maps formulas to formulas. In particular, it maps formulas of the form $P \believes \phi$ to $P \rightlybelieves \phi$.It is defined as follows:

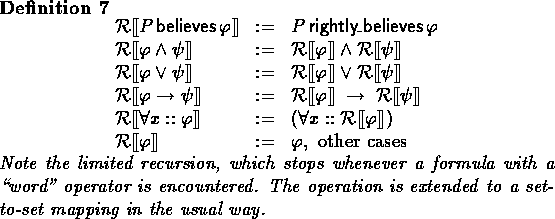
Directly from the definition on sets it follows that:

 

 

Proof

We prove it with structural induction on the derivation.

Case trivial proof: A trivial proof is a derivation step of the form ${\cal A} \derives {\cal C}$, where ${\cal C}\subseteq{\cal A}$.

Case deduction: Deduction is the introduction of implication by derivation:

If $\varphi \derives \psi$, then $\derives \varphi \implies \psi$.

Using deduction, we may instantiate:

If $\rectify{\varphi} \derives \rectify{\psi}$, then $\derives \rectify{\varphi} \implies \rectify{\psi}$.

From here we can derive, under the assumption $\rectify{\varphi} \derives \rectify{\psi}$:

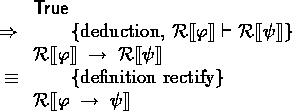
Cases axioms of predicate logic: As an example, we prove our claim for the introduction of $\land$.Other introductions and eliminations ($\lor$, $\implies$, $\neg$, $\forall$)have analogous proofs.

Case Rationality: Let $\derives \varphi$. We prove $\derives \rectify{P \believes \varphi}$.

Case axiom:

For every axiom $\derives \varphi \implies \psi$, we will prove $\derives \rectify{\varphi \implies \psi}$, by deriving $\rectify{\varphi} \derives \rectify{\psi}$.

case Believing Modus Ponens: We prove it for the equivalent form $\derives (P \believes (\varphi \implies \psi) \land P \believes \varphi) \implies P \believes \psi$

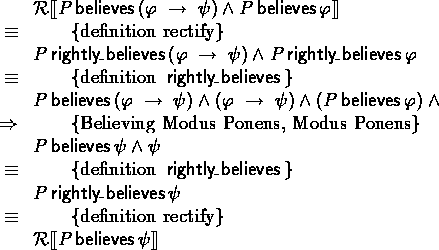
case Saying contents of an encrypted message:

case Awareness:

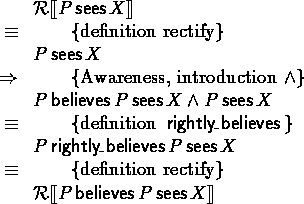
case Possessing believed keys:

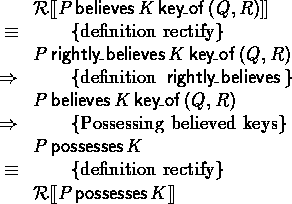
The remaining axioms do not contain a believe operator, so they do not change under the rectify function.