
|
Points on a Parabola Chromatic number of the Plane |
 RESEARCHER: Nate Dean
RESEARCHER: Nate DeanOf course, since this is an open problem, no-one can claim to know just what field the problem lies in, since no-one knows the solution.
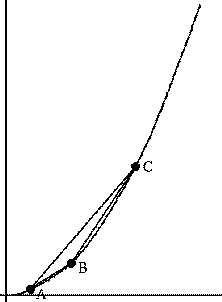
I believe it is not even known if there are more than 5 points on the parabola which satisfy the condition. It is certainly not known if there is an infinite family with pairwise rational distances. We can quickly see that there are three such points in the following way: Pick two rational numbers, say 1/5 and 3/5, and let those be the distances between the pairs of points AB and BC. If you fix those distances and slide the points up the parabola, the distance AC will gradually increase, bounded above by 4/5. Since the rational numbers are dense in the reals, there will be many placements of the points so that AC is a rational distance.
It is not too hard to show that if you have N points on the parabola with rational distances between them, then you can find N points on the parabola with integer distances between them.
 RESEARCHER: Robert Hochberg
RESEARCHER: Robert HochbergThis problem is closely related to the problem of finding unit distance graphs with large chromatic number. This problem has been open since it was first posed by Edward Nelson in 1956. At that time, it was proved that the chromatic number of the plane was either 4, 5, 6 or 7, and no improvements on those bounds have been made since! The coloring of the plane shown to the right, where each square has side 3/5, shows that the chromatic number of the plane is at most 9. Can you find a coloring with 7 colors to get the current best-known upper bound?
This problem is very hard, judging by the length of time that has gone by with no improvements on the bounds. It will probably take some brand new idea to make a contribution. So, what are you waiting for?!