Graph Theory Open Problems
Index of Problems
Unit Distance Graphs---chromatic number
RESEARCHER: Robert Hochberg
OFFICE: CoRE 414
Email:hochberg@dimacs.rutgers.edu
DESCRIPTION: How many colors are needed so that if each point in the
plane is assigned one of the colors, no two points which are exactly distance
1 apart will be assigned the same color? This problem has been open since
1956. It is known that the answer is either 4, 5, 6 or 7---this is not too
hard to show. You should try it now in order to get a flavor for what this
problem is really asking. This number is also called ``the chromatic number
of the plane.''
A graph which can be embedded in the plane so that vertices correspond
to points in the plane and edges correspond to unit-length line segments
is called a ``unit-distance graph.'' The question above is equivalent to
asking what the chromatic number of unit-distance graphs can be.
Here are some warm-up questions, whose answers are known: What complete
bipartite graphs are unit-distance graphs? What's the smallest 4-chromatic
unit-distance graph? Show that the Petersen graph is a unit-distance graph.

Unit Distance Graphs---girth
 RESEARCHER: Robert Hochberg
RESEARCHER: Robert Hochberg
OFFICE: CoRE 414
Email:hochberg@dimacs.rutgers.edu
DESCRIPTION: As the problem mentioned above remains unsolved, mathematicians
have turned their attention to related problems in the hopes of gaining some
insight into this difficult question.
In this problem, we are interested in finding what sort of unit-distance
graphs we can make--in particular, can we find 4-chromatic graphs which have
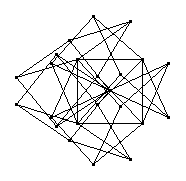
large girth? Paul O'Donnell has found a unit distance graph of girth 12
which cannot be 3-colored, but this graph has an incredibly large number
of points. Hochberg and O'Donnell have found 4-chromatic unit-distance graphs
of girths 4 and 5 with 23 (shown to the right) and 45 vertices respectively. Are there smaller ones?
Are there 4-chromatic unit-distance graphs of arbitrarily large girth?
An answer to this question may help to solve the "chromatic number of the
plane" problem.

Barnette's Conjecture
 RESEARCHER: Peter Hamburger
RESEARCHER: Peter Hamburger
OFFICE: CoRE 442
Email:hamburge@dimacs.rutgers.edu
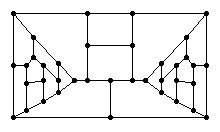
DESCRIPTION: Is it true that every 3-connected, 3-regular, planar
bipartite graph is Hamiltonian?
It is known that this is not true if you remove the "bipartite" condition,
but the smallest known such graph which is not Hamiltonian has 38 vertices,
as shown to the right.

Crossing Number of K(9, 9)
 RESEARCHER: Robert Hochberg
RESEARCHER: Robert Hochberg
OFFICE: CoRE 414
Email:hochberg@dimacs.rutgers.edu
DESCRIPTION: What is the crossing number of the complete bipartite
graph K(9, 9)? It is conjectured to be 256, but nobody knows.
Another way to ask this is the following: If you place 9 red points in
the plane and 9 blue points in the plane, and then connect each red point
to each blue point with curves (81 curves in all), then what is the minimum
number of crossing points that must appear in your drawing?
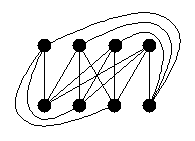
An example for K(4,4) is shown to the right, with 8 crossings. Actually,
this graph can be drawn with just 4 crossings...can you find it?
For these drawings, it is assumed that the curves do not touch the points
(vertices) except at their endpoints, and that no three curves meet at a
point.

Vertices and Neighbors on a Cycle
 RESEARCHER: Nate Dean
RESEARCHER: Nate Dean
OFFICE: Chair of Mathematics, Texas Southern University
Email: dean_nx@tsu.edu
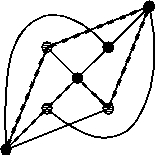
DESCRIPTION: Is it true that every k-connected (k>1) graph which
does not have a Hamiltonian cycle has a cycle that contains k independent
vertices and their neighbors? This is known to be true for k = 2 and 3.
For example, the graph to the right is 3-connected but not Hamiltonian.
And the dotted cycle shown contains 3 independent vertices (the three vertices
which are lighter in color) and thier neighbors. To see that it is not Hamiltonian,
notice that this graph is just the complete bipartite graph K(3,4).

The Square of a Directed Graph
RESEARCHER: Nate Dean
 OFFICE: Chair of Mathematics, Texas Southern University
OFFICE: Chair of Mathematics, Texas Southern University
Email: dean_nx@tsu.edu
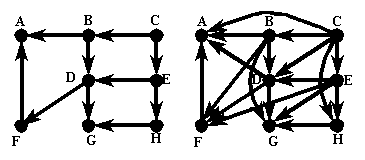
DESCRIPTION: This problem deals with the "square of an oriented graph."
An oriented graph is a simple graph (no loops or multiple edges) in which
each edge is replaced by an arc. Thus you produce a simple directed graph
without pairs of "reversed arcs."
To get the square of an oriented graph (or any directed graph) you leave
the vertex set the same, keep all the arcs, and for each pair of arcs of
the form (u,v), (v,w), you add the arc (u,w) if that arc was not already
present. An example of an oriented graph and its square is shown above.
Here is the open problem: Prove that for every oriented graph, D, there
exists a vertex whose out-degree at least doubles when you square the oriented
graph. In the example above, the vertices A, B, C, E and G satisfy this
property. (For vertices A and G, 2*0=0). Nate learned of this problem
from Paul Seymour. David Fisher proved this theorem for tournaments, i.e.,
orientations of complete graphs.



 RESEARCHER: Peter Hamburger
RESEARCHER: Peter Hamburger
 RESEARCHER: Robert Hochberg
RESEARCHER: Robert Hochberg RESEARCHER: Nate Dean
RESEARCHER: Nate Dean OFFICE: Chair of Mathematics, Texas Southern University
OFFICE: Chair of Mathematics, Texas Southern University