Let ![]() be the secret key to be discovered. We
suppose that exponentiations are achieved by the right-to-left
square-and-multiply algorithm (Fig. 3). The attack
supposes that the register containing the value of y has some
permanently damaged known bits, always `0' or `1'. Let
be the secret key to be discovered. We
suppose that exponentiations are achieved by the right-to-left
square-and-multiply algorithm (Fig. 3). The attack
supposes that the register containing the value of y has some
permanently damaged known bits, always `0' or `1'. Let ![]() and
and ![]() denote the subsets of correct and incorrect
(i.e. damaged) bits of register y , respectively. So, any value
denote the subsets of correct and incorrect
(i.e. damaged) bits of register y , respectively. So, any value ![]() stored in register y can be written as
stored in register y can be written as![]()
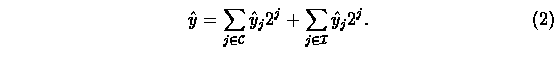
From Eq. (1), the faulty signature corresponding to message m is given by
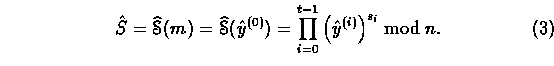
Let ![]() be the function that maps the
correct bits of
be the function that maps the
correct bits of ![]() to the correct bits of
to the correct bits of
![]() . Since
. Since ![]() is finite, the sequence must
eventually cycle. The length
is finite, the sequence must
eventually cycle. The length ![]() of the tail and
the length
of the tail and
the length ![]() of the cycle can efficiently be computed by the
Floyd's algorithm [9, exercise 6 on p. 7]. This algorithm is
also known as the kangaroos' method . It has the advantage of
minimizing the storage requirements.
of the cycle can efficiently be computed by the
Floyd's algorithm [9, exercise 6 on p. 7]. This algorithm is
also known as the kangaroos' method . It has the advantage of
minimizing the storage requirements.
Two kangaroos ![]() and
and ![]() cover the sequence generated by f .
Kangaroo
cover the sequence generated by f .
Kangaroo ![]() progresses in bounds of 1 unit and kangaroo
progresses in bounds of 1 unit and kangaroo ![]() in
bounds of 2 units. Since the sequence cycles, the two kangaroos will
meet. If they meet after k bounds, then
in
bounds of 2 units. Since the sequence cycles, the two kangaroos will
meet. If they meet after k bounds, then
![]() . Once k has been found, it suffices
to generate
. Once k has been found, it suffices
to generate ![]() and
and ![]() for
for ![]() .Then,
.Then, ![]() is the smallest integer j such that
is the smallest integer j such that
![]() .
.
Proof.Since ![]() , it follows that (2k-k) is a
multiple of
, it follows that (2k-k) is a
multiple of ![]() . Moreover since
. Moreover since
![]() ,
, ![]() is the smallest
integer j such that
is the smallest
integer j such that ![]() .
.![]()
length ![]() of the cycle is the smallest integer j such
that
of the cycle is the smallest integer j such
that ![]() . Putting all together, we obtain
the Floyd's algorithm (see Fig. 5).
. Putting all together, we obtain
the Floyd's algorithm (see Fig. 5).
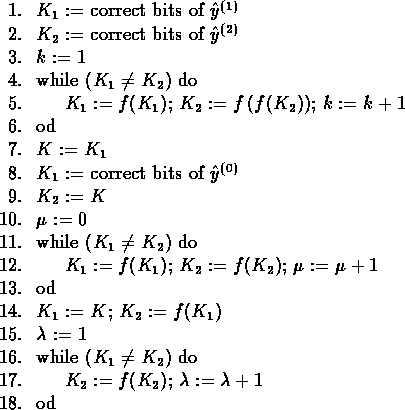
To recover the bits of the secret exponent s , the pirate Carol
proceeds as follows. She first chooses a random message m . Then, by
the kangaroos' method, she computes the tail's length ![]() and the
cycle's length
and the
cycle's length ![]() of the sequence generated by the
of the sequence generated by the
![]() . If the sequence does not cycle, she chooses another
message m and reiterates the process. The first bit of s is
. If the sequence does not cycle, she chooses another
message m and reiterates the process. The first bit of s is
![]() since s must be odd. To find the next
since s must be odd. To find the next ![]() bits
bits
![]() , Carol asks to Alice to sign some
, Carol asks to Alice to sign some
![]() and successively evaluates
and successively evaluates
If ![]() then
then ![]() ;otherwise
;otherwise ![]() .
.
Proof.Assume that Carol already computed
![]() and therefore knows
and therefore knows
![]() . Then, she computes
. Then, she computes
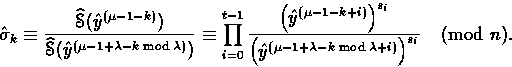
Suppose that ![]() . Then letting i=k+1+j with
. Then letting i=k+1+j with ![]() , we have
, we have
![]()
and
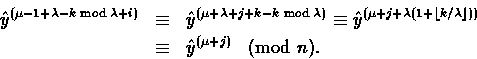
So,
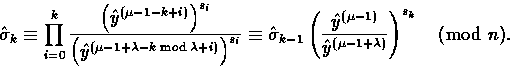
![]()
There is no general recipe to find the remaining bits of s . If the
length ![]() of the tail is short, Carol may choose another
random message m to find the
of the tail is short, Carol may choose another
random message m to find the ![]() first bits of s . The next bits
have to be found by exhaustive search. However, this search can be
speeded up by noting that the unknown bits have to fulfill some
algebraic relations.
For example, the bits
first bits of s . The next bits
have to be found by exhaustive search. However, this search can be
speeded up by noting that the unknown bits have to fulfill some
algebraic relations.
For example, the bits ![]() must satisfy
the following relations:
must satisfy
the following relations:
and
Proof.
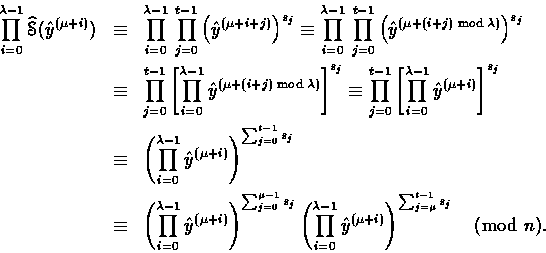
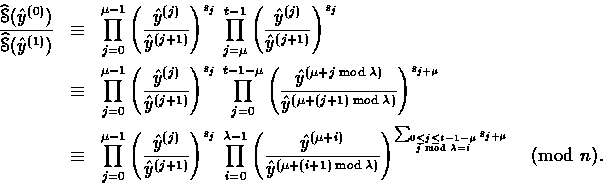
![]()
Note that if ![]() , then Eq. (6) simplifies to
, then Eq. (6) simplifies to
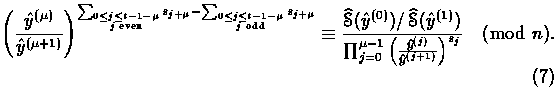
Similar relations can be exhibited if ![]() is a power of 2.
is a power of 2.