
The datatype used to model the possible messages is given by

where TEXT , NONCE , and USER are all primitive sets. The set KEY further subdivides into SESSION and LONGTERM , representing two different ways in which keys are used: typically, session keys are only used for a single run of the protocol, whereas longterm keys are used repeatedly.
![]()
If ![]() are arbitrary messages, and k is a key, then the
generates relation
are arbitrary messages, and k is a key, then the
generates relation ![]() for this message space is defined by the following
rules:
for this message space is defined by the following
rules:
Observe that hashing is one-way: there is no rule which allows information to be extracted from a hashed message. Observe also that all keys in this protocol are symmetric: knowledge of a key allows any message encrypted with that key to be decrypted.
The protocol describes the required behaviour of each of its participants. We will use CSP processes to describe the behaviour of each of the participating agents. For simplicity, we will consider in this paper a single run of the protocol, though the approach extends naturally to multiple concurrent runs, as discussed in [Sch96].
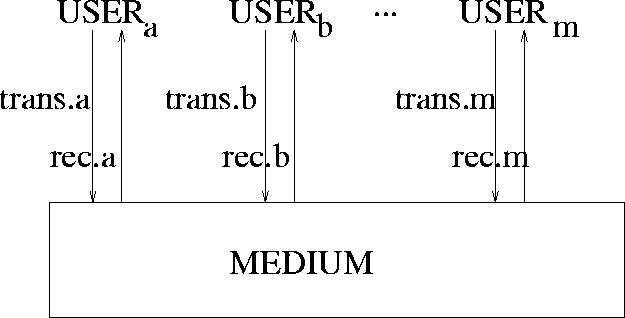
We model an agent i as sending all of its messages on to the medium and receiving all its messages from the medium through the channels trans.i and rec.i respectively, as illustrated in Figure 1.
Messages on these channels have the type USER.USER.MESSAGE , where
USER is the set of all protocol agents names, trans.i.j.m
represents the transmission onto the medium of message m from
![]() addressed to
addressed to ![]() , and rec.i.j.m represents the
reception of message m by
, and rec.i.j.m represents the
reception of message m by ![]() , labelled as coming from
, labelled as coming from
![]() . The message m is drawn from the abstract data-type
MESSAGE . The users are defined according to the protocol that
we are analysing.
. The message m is drawn from the abstract data-type
MESSAGE . The users are defined according to the protocol that
we are analysing.
Figure 1:
CSP model of the network
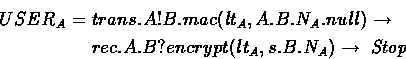
where ![]() is a fresh nonce. Agent A transmits an initiating
request to agent B on channel trans.A and awaits a reply on
channel rec.A .
is a fresh nonce. Agent A transmits an initiating
request to agent B on channel trans.A and awaits a reply on
channel rec.A .
The freshness of ![]() is modelled by the fact that it is not
initially known by the enemy:
is modelled by the fact that it is not
initially known by the enemy: ![]() , where INIT will be
used to model the
information known by the enemy at the start of the protocol run.
, where INIT will be
used to model the
information known by the enemy at the start of the protocol run.
After sending out the initial request, the process is prepared to
accept any message which is labelled as coming from B , is encrypted
with its long term key and contains both its nonce challenge ![]() and
the agent B 's identity. It will accept the key s as a session key
generated by the server for private use between A and B .
and
the agent B 's identity. It will accept the key s as a session key
generated by the server for private use between A and B .
Intermediate nodes along the chain all have the same form. If the node next up the chain from B is C then the appropriate description is as follows:
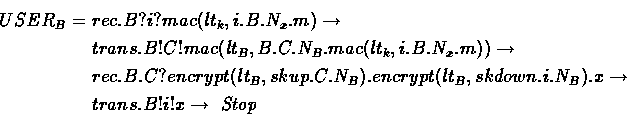
Agent B receives a request from some agent, which it packages suitably and sends on to its successor (Agent C in this case.) It then receives a message consisting of a list of key certificates. The first two certificates contain sessions keys for communication with the agent immediately below (skdown ) and above (skup ). The rest of the message is passed to the agent i from whom the original request was received.
The server inputs a message which consists of a nested series of requests, and then outputs a message which is a concatenation of all of the key certificates encrypted for the appropriate agents.
![]()
The function response defined on the possible legitimate requests that may arrive at the server is defined inductively as follows:

The session keys ![]() generated by the server are all fresh and
unguessable: none appear in the set INIT .
generated by the server are all fresh and
unguessable: none appear in the set INIT .
The protocol operates in a hostile environment. This is also modelled within CSP in order to facilitate analysis. The approach taken is to provide a CSP description of the Dolev-Yao model [DY83]. In this model, it is assumed that the medium is under the complete control of the enemy, which can block, re-address, duplicate and fake messages.
The network description consists of a set of user processes which execute the protocol, an intruder process and a medium which carries all the messages.
As is pointed out in [Sch96], the medium and intruder can be rewritten as a single process ENEMY :
This is the description we shall use through this paper: ENEMY =
ENEMY(INIT) , where INIT does not contain ![]() ,
, ![]() ,
, ![]() ,
, ![]() or
or ![]() .
.
Although this description looks simple, it is powerful enough to model all aspects of the Dolev-Yao model, in that it can block, duplicate, re-order or fake messages. All attacks involving these operations are therefore possible within the model.