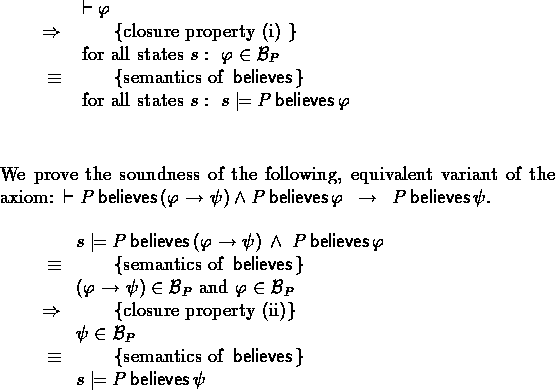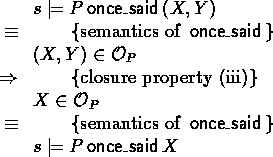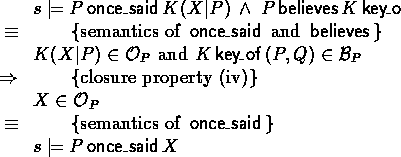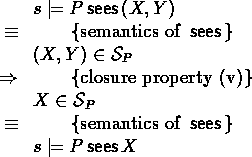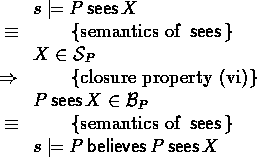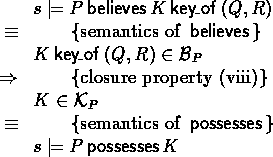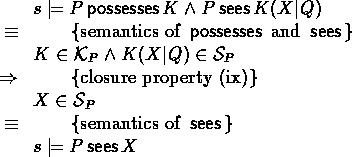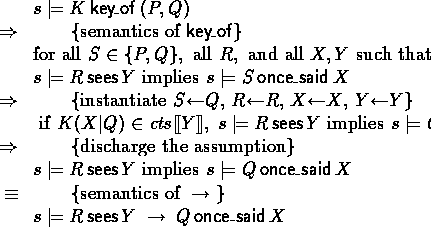

Next: Protocols
Up: A semantics for BAN
Previous: Semantics of formulas
![\begin{theorem}[Soundness]
The logic as described in this article is sound with respect to the
newly defined semantics.\end{theorem}](img136.gif)
Proof of Theorem 11
For each axiom 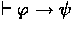 ,as summed up in section 2.2,
we prove
,as summed up in section 2.2,
we prove 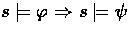 .
.
- Rationality
- does not have the form
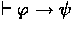 ; instead, we have to show
that for each theorem
; instead, we have to show
that for each theorem 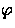 (and any P in the environment)
the formula
(and any P in the environment)
the formula  is a tautology.
is a tautology.
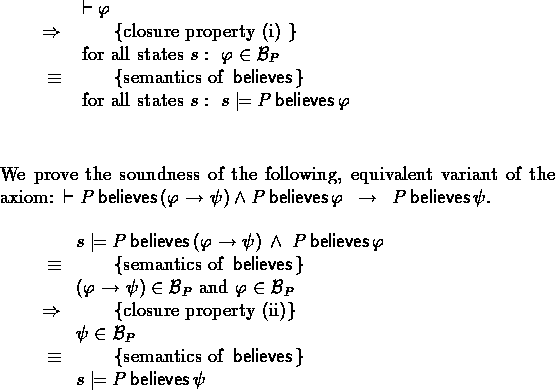
- Saying parts of a joint message
-
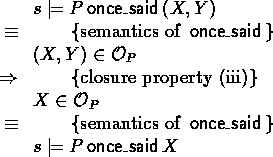
- Saying contents of an encrypted message
-
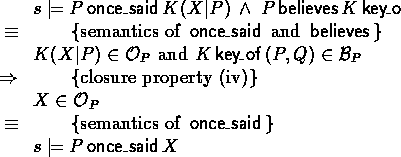
- Seeing parts of a joint message
-
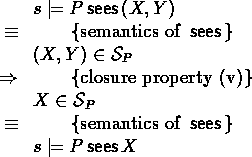
- Awareness
-
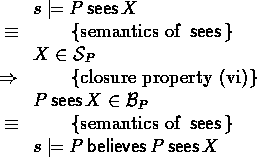
- Possessing keys of a seen key statement
-

- Possessing believed keys
-
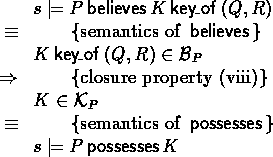
- Decryption
-
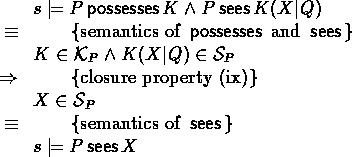
- Good key ensures the utterer
- We prove the soundness of this equivalent variant of the
axiom:
 ,where we may use the assumption that
,where we may use the assumption that 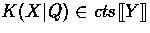 :
:
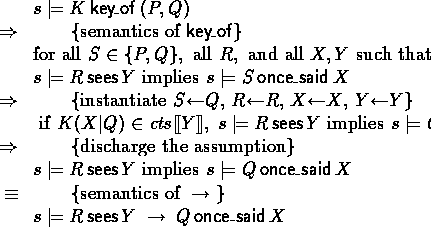

![]()
![]() ,as summed up in section 2.2,
we prove
,as summed up in section 2.2,
we prove ![]() .
.