This section presents separate weakest preconditions for decryption using each of the available key types: shared keys, public keys, private keys, and shared secrets. The notation used is:

Table 8: B decrypts a generically encrypted message ( ![]() ) using a key
(K).
) using a key
(K).

Table 9: B decrypts a message ({X} ![]() ) using B's private key
(K
) using B's private key
(K ![]() ).
).
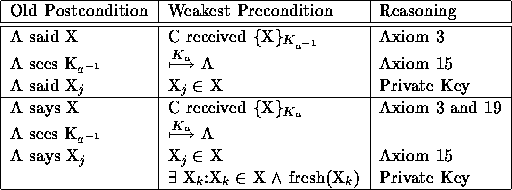
Table 10: B decrypts a message ({X}) using A's public key
(K ![]() ).
).
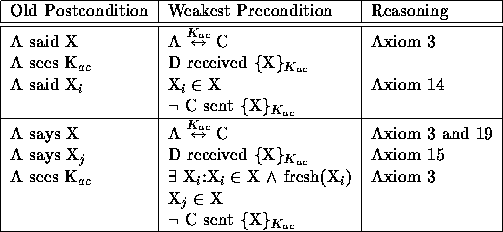
Table 11: B decrypts a message ({X} ![]() ) using a shared key
(K
) using a shared key
(K ![]() ).
).
Table 8 lists the wps that are the same for all three key types. These treat decryption like a function and do not require the validity of the key. The next three tables show the unique wps for each key type: private (Table 9), public (Table 10), and shared (Table 11). These are used for determining the sender of the message and do depend upon the validity of the key (and possibly validity of a shared secret).
For messages encrypted with the public half of a public-private pair the signature depends on a valid shared secret and knowledge of who didn't send the message. Although the decrypting party doesn't have to share the shared secret in any reasonable protocol they will. For messages encrypted with the private half of a public-private pair the message is effectively signed automatically.
Messages encrypted with a shared key use the knowledge of who didn't send the message to determine the sender. This may be a difficult use of a not as it requires determining that the given condition is not within the set of conditions. In deriving a protocol from a set of postconditions this would mean checking each operation to assure that it didn't introduce the condition.