While Mr. Johnson is meeting with some of the children in his first-grade class, others are involved in a number of different activities. At the Math Center, pairs of students have cups with eleven chips that are yellow on one side and red on the other. As each pair pours out the chips, they write a number sentence showing how many yellows and how many reds they got, as well as the total. When they have written ten number sentences each, they move on to another activity.

The students:

work on basic facts in the context of a problem and in relation to other areas of mathematics.

work in pairs with manipulatives.

Later in the day, as Mr. Johnson begins the math lesson, he asks the students to recall their discussion from the previous day, "What were we talking about yesterday in math?"

practice their number facts by writing down each result.

"We were doing numbers that add up to eleven, like 5+6 and 2+9," answers Clark.

"Or 3+8 and 4+7," adds Sarah.

"Is there more than one way to get a sum of eleven?"

share mathematical ideas.

Mr. Johnson lists all of the children's responses on the board. He goes on to ask them, "What were you doing at the Math Center earlier today?"

Jackie responds, "We were tossing counters and writing number sentences."

"We were tossing eleven counters!" says Toni.

"What can you tell me about your results?" asks Mr. Johnson. "Did you get the same number sentences as your partner?"

"No - we got different ones!"

connect their understanding of one mathematical idea to another.

"Our answers were always the same - eleven!"

"I got some number sentences more than once!"

"I got 5+6 three times!"

"I didn't get 0+11 or 11+0 at all!"

report and reflect on the differences of their results.

"Why do you think you got different answers?" asks Mr. Johnson. He listens as the students talk about fairness, luck, and chance, pointing out that all of the counters are alike. The students agree finally that the different number sentences are a result of chance.

The students continue their discussion of which number sentences appear more often than others. One of the children suggests that maybe they should make a graph to help them see which number sentences occur most often. Mr. Johnson thinks that this is a good idea. He goes through their list of number sentences, asking students to raise one finger if they got that number sentence once, two fingers if they got it twice, and so on. For each finger raised, he puts a tally mark on the board. When they are done, he asks whether there were any other number sentences that anyone got. Then the children look at the general shape of the data, noticing that most of the number sentences were in the middle. Mr. Johnsonpoints out that not all of the number sentences are equally likely to occur. He says that tomorrow they will have a chance to play a game with the counters in which they will need to select which number sentences will be winners. Tomorrow's activity will continue providing opportunities for practicing basic facts while building on the beginning ideas of probability.

informally explore the concepts of probability.

use different methods to display data.

make inferences about their data.

Mr. Marshall had assigned the following problem from the New Jersey Early Warning Test as a homework assignment for his fourth grade class:

Use each of the digits 3, 4, 5, 6, 7, and 8 once and only once to form three-digit numbers that will give the largest possible sum when they are added. Show your work.

Is more than one answer possible? Explain your answer.

The students:

are asked to respond to open-ended questions and present and defend their solutions.

The students were to solve the problem and match their response with that of Tilly Tester to see if they agree or disagree with Tilly's response and explain why.

are asked to analyze problems for reasonableness of results and to diagnose errors.

As the math class begins, Mr. Marshall allows the students to work in the cooperative learning groups which they have been working with this month to compare the results of their homework assignment. Mr. Marshall visits each group noting who has completed the assignment as well as the direction of the discussion for each group. Homework assignments are important and students are given credit for homework. Strategies such as displaying answers on the overhead projector and working in cooperative learning groups are used to ensure that homework review is no more than 5 to 10 minutes.

work cooperatively to assess their own and each other's work.

Mr. Marshall then asks the students to show the level of their agreement with Tilly's response on a 0-5 scale, with 0 signifying disagreement and 5 signifying total agreement. Most students raise 4 or 5 fingers, and the discussion then focuses on how Tilly's answer could be improved. One group notes that Tilly should have added each pair of numbers and shown the sum for each, while another group explains that Tilly could have also changed the hundreds place to get 754+863 and 763+854.

are willing to take a position without the fear of being incorrect.

At this point, Mr. Marshall discusses Tilly's understanding of place value and uses the opportunity to summarize the students' responses and lead into the objective of the day which focuses on place value and multiplication.

use their knowledge of numeration to help solve problems.

"Let's work on multiplication today, and to get started, let's do some mental math with multiplication. On the back of your homework, number 1 to 10. Write the answers only for my mental math flashcards."

Individually, the students write answers for 8000x3, 6000x7+50, 300x7, etc. After the ten problems, Mr. Marshall has the students exchange papers, and they correct and discuss the answers. The papers are collected, and Mr. Marshall poses the following problem for his students:

Use four of these five digits and construct the multiplication problem that gives the greatest product: 1, 3, 5, 7, 9

use mental math regularly throughout the curriculum.

demonstrate their understanding of mathematical concepts in a variety of ways, each of which provides valuable assessment information to the teacher.

Before allowing the students to start work on the problem, he asks them to estimate what the largest product obtained in this manner might be. Students offer estimates ranging from 3000 to 10,000 and provide explanations for their guesses. When allowed to, the class works in their cooperative learning groups. Calculators are available, and some students start guessing and checking with their calculators.

are encouraged to estimate solutions before actually determining answers.

use calculators to aid in the problem-solving process.

One group begins to discuss which digits to use, wondering whether there would be a reason not to use the four largest digits. Another group is discussing whether a 2-by-2 or a 1-by-3 arrangement would be the best for getting a large product, an aspect of the problem that some groups have completely missed. Most of the groups get around to trying out sample problems of a variety of sorts to get some parameters worked out. Toward the end of the class session, the groups share the specific answers they have come up with. The three examples that are suggested are:

    753    93    953
  x   9  x 75  x   7
  -----  ----  -----
   6777  6975   6671

using mathematical reasoning to formulate strategies and solutions.

It is clear to everyone that the 2-by-2 digit problem is the one with the greatest product, but Mr. Marshall is looking for some generalizations that can be made. He points out that none of the groups used the digit "1" in their examples. Can the lowest digit always be ruled out? He asks the groups that arrived at the 2-digit problem to explain how they decided where to put the individual digits. Does it matter where they were placed? Where does the largest one go? The smallest? Do you think it would always work that way regardless of what the individual digits were? How can you check? The students reflexively pick up their calculators and begin to formulate other versions of the problem that use other digits and to check which arrangements of the digits give the largest product. One student asks his partners what they think would happen if two or three digits were the same.

approach numerical operations from a holistic point of view rather than only through paper-and-pencil manipulation.

For homework, Mr. Marshall asks the students to use the same five digits, but to find the smallest possible product. They are then to write a paragraph describing their solution and the reasoning they used to show it is, indeed, the smallest product. Specifically, they are to consider the question: Can you just turn your thinking about the way you got the largest product upside down and use it to get the smallest product?

write paragraphs describing and justifying their positions.

Today is November 12 and Maria, a student in Miss Palmer's second grade class is very excited. Today is Maria's birthday, and as is the custom in her class, she is bringing in a birthday snack to share with her classmates. Maria and her father spent much of the previous evening making a batch of chocolate chip cookies and she proudly walks into class carrying a cannister full to the brim. Miss Palmer realizes that she can use mathematics to help the class divide the cookies.

Before the afternoon snack time, Miss Palmer poses the problem to the whole class.

The students:

use mathematics to devise a solution for real-world problems.

Miss Palmer states, "Today is Maria's birthday and she has brought in some delicious chocolate chip cookies for all of us to enjoy at snack time. Maria told me she baked a whole bunch of cookies. I would like us to think about how we could determine the number of cookies each student in the class should get. Discuss it with your partner."

use cooperative work to generate potential solutions.

The students begin to discuss all of their ideas. After a few minutes, Miss Palmer calls on a few of the students. As they share their ideas, the teacher records them on the language experience chart.

Sarah states, "Well, me and Mario think that the first thing we have to do is count the cookies to find out how many there are."

Jerome adds, "Yeah, and we also need to know how many children are in the class today."

"That's easy. I did the lunch count this morning and there are 22 children in school today," Maria volunteers.

Luis chimes in. "Once we know how many cookies and how many children, then we can figure out a way to solve the problem."

The children all agreed that since they know there are 22 children in class today, the next step was to determine the number of cookies. Miss Palmer highlights that idea on the language experience chart and gives each pair of children a bag of counters which represents the number of cookies.

regularly share their ideas publicly.

Miss Palmer says, "Each pair of children received a bag of counters. I want you to pretend that these are Maria's cookies. I've counted the cookies. The number of counters in each bag is equal to the number of cookies Maria brought for a snack. With your partner, use your counters to first decide how many cookies Maria brought to school and then determine how many cookies each student will get if the cookies are to be shared equally among everyone in the class. When you are finished, each pair will need to write a story which explains how both of you solved the problem."

use manipulatives to model real-world situations.

The children worked with their regular partners. The first task they all tackled was to count the number of counters in each bag. Most of the pairs of children counted by twos to determine the total number of counters was 62. However, Alex and Laura kept losing count when trying to count all the counters and decided to group the counters by ten. Miss Palmer was delighted to see that most pairs of children had written the total number of counters (62) on a sheet of paper. She had been stressing the importance of collecting data and recording information.

As Miss Palmer continued to circulate around the classroom, she noticed the children were solving thesharing problem in various ways.

use their knowledge of decimal place value to simplify the task.

One pair of students begins by drawing 22 stick figures to stand for the students in the class and then starts to "give out" the cookies by drawing them in their stick figures' hands. Another pair also starts with 22 stick figures but then draws 62 little cookies on another part of the paper and is stumped about where to go from there. Mario and Sarah begin to sort the 62 counters into 22 piles. Another pair, trying to use calculators to solve the problem, starts by adding 22 cookies for everyone to another 22 cookies for everyone to a third 22 cookies for everyone and then realizes that they have exceeded the number of cookies available.

Miss Palmer, noticing that the students will be unable to finish the problem before they have to go to Physical Education, calls the students back together.

"I want all of you to stop what you are doing, and with your partner write a story to tell me how you are attempting to solve this problem," she directs.

develop their own methods for solving the problem.

use technology as a problem-solving tool.

The students eagerly write their stories. Some use pictures to help illustrate their solutions.

Miss Palmer requests, "I would like some of the pairs to report to the whole class how they were attempting to solve the problem."

draw pictures to model their solutions.

Luis states, "Well, Elizabeth and I figured out that each student could have 2 cookies and there will be 18 cookies left. We know this because we drew a picture of the class and put counters on each student. When we couldn't give counters to every kid, we decided those were leftovers and we counted them."

Lisa volunteers, "We drew stick figures too. After we gave out 2 cookies to each child, Jerome said we couldn't give out the 18 leftovers. But I think we can break the leftover cookies in half. Then each child would get 2 whole cookies and one half cookie. But I'm not sure how many would be left over then."

"Sarah and I used the calculator to solve the problem. We put in 62 and I counted while Sarah subtracted 22. We got 2 with 18 left over," Mario added.

"Alex and I got a different answer. We used the counters and put them into 22 piles, but we got 17 leftovers," Laura said.

Lisa suggested, "Maybe you and Alex should count them again to make sure you have the right number in each pile."

give explanations of their strategies for solving the problem.

informally explore the uses of fractions and notions of fair sharing.

Laura and Alex recount their piles and discover that one counter fell on the floor.

Vanessa states, "Me and my partner thought of another way of sharing the leftover cookies. Everyone could write their name on a piece of paper, then put all the papers into a bag and have Maria close her eyes and pick out 18 names. Those kids would get the extra cookies."

Sarah protested, "We forgot about Miss Palmer. We should give her 2 cookies and that would leave 16 left over. Maria could give them to the principal and the other ladies in the office."

Miss Palmer wrapped up the discussion. "We've discussed many ideas for sharing the 62 cookies Maria brought for a snack. On the back of the sheet of paper I gave you, I would like you and your partner to decide on how you think we could fairly share the cookies."

are mutually supportive and regularly offer feedback to each other.

The children work on their final summary of the problem and hand their papers in before getting on line for Physical Education. While the children are in Physical Education, Miss Palmer reads the children's solutions. She makes notes on the cards she keeps for each child. This will help her better understand various developmental levels of her students. She notices that Vanessa has really made progress since September. Laura and Alex still like to "rush" to finish their work. She makes a note on their paper encouraging them not to be so concerned about being the first ones finished. Overall, she feels encouraged, not only about the solutions to the problems, but also about the ways in which her class has learned to communicate their ideas both orally and on paper. She decides to let the class choose one of the methods suggested to distribute the cookies at snack time.

demonstrate their understanding of mathematical concepts in a variety of ways, each of which provides valuable assessment information to the teacher.

Mr. Santos' 6th grade class has just completed a review of place value in the decimal number system and he is preparing to start a unit introducing exponents. He has coordinated the timing of this unit with the language arts teacher whose class is in the midst of a unit on fables. One fable they have read involves a knight who saves a kingdom from a horrendous dragon. Given the opportunity to determine his own reward, he tells the king that he would take one penny on the first square of a chessboard, two pennies on the second, four pennies on the third, and so forth until each square on the chessboard has twice as many as the previous one. Mr. Santos has the students recall the story and then asks the students to determine how much money the knight would make with this method of payment.

The students:

are connecting a language arts experience to their mathematics learning.

Mary said, "We need to know how many squares there are on a chessboard before we can do this problem."

are comfortable taking risks.

Lionel stated, "Give me a minute to think. I play on the chess team, but I need to take a moment to picture it. Let's see, I know it's square and there are 1,2,3, ...8 squares along the one side. There are 64 squares!"

Jerry shouted, "He gets 128 pennies. Two on each square."

use known facts to explain their thinking.

"The fable doesn't say he gets two on each square! It says that each square has twice as many as the one before. It has to be more than 128!" corrected Meredith.

react substantively to others' comments.

"We need to examine this situation in some organized fashion. I want you to get in your groups of four and determine the people who will serve the usual roles of leader, recorder, reporter, and analyzer of group interaction," stated Mr. Santos.

use standard cooperative learning strategies.

One group decided to develop a computer program which printed a table listing the number of the square, the number of coins on that square, and a subtotal to that point.

use technology to help solve the problem.

Another group borrowed the class chessboard and began placing play coins on the squares. It soon became obvious to them that they would not have enough play money to complete this attempt. They started to make a table with the information they had constructed and worked to find a pattern which they could extend to the complete board. Their table only included columns showing the number of the square, the number of coins on that square, and a column to list patterns. They discovered that the number of coins could be represented by raising 2 to the power which was one less than the number of the square. Using calculators, they found the number of coins on each square and then the total number of coins.

Another group began making a table similar to the group above, but they also included a column showing the partial sums and another which attempted to find a pattern in the partial sums. Eventually, they discovered that the partial sum at each square was one less than 2 raised to the power equal to the number of the square. They could then quickly utilize the calculators to compute the total.

concretely model the problem before they move on to more symbolic procedures.

use self-assessment to determine the effectiveness of their method.

analyze mathematical situations by recognizing and using patterns and relationships.

At the end of the period, Mr. Santos reminded the groups that they were to prepare a report of their methods which included a description of their processes, an explanation of why they chose them, and their evaluation of their processes. He asked each of them to consider the magnitude of their answer and find some way to explain to another person just how large the answer was. Students brainstormedsome ideas such as the distance between two known points or objects, the magnitude of the national debt, and the number of people on earth.

choose technology to reduce the computational load.

write about their approaches and solutions to problems.

connect their knowledge of mathematics to the real world.

Ms. Ramirez announces to her seventh grade class that in three weeks they will make a journey to Trenton, the capital of New Jersey. They will be visiting eight sites - the Capitol, the New Jersey Museum, the War Memorial, the Old Graveyard, Trent House, the Old Barracks Museum, the Firehouse, and the Pedestrian Mall. To ensure that they spend as much time at the sites as possible, and do as little walking as possible, the class must find the most efficient walking tour for the trip, starting and ending at the parking lot.

The students:

apply mathematical skills to solve a real-world problem.

The first problem that the students must address is finding the walking distance between each pair of sites. Ms. Ramirez supplies each team with a street map and a ruler; the maps identify all the sites to be visited and the routes joining them. She assigns each group the task of finding the distances between one site and all the others. This turns out to be an interesting task, since different groups interpret it differently. Some groups, for example, measure the straight line distance between two sites forgetting that buildings or ponds might render that walk impossible. How to measure the walking distance thus becomes an important topic of discussion, as does the question of appropriate units. These questions are eventually settled and the teacher uses the students' measurements to write a matrix which indicates the walking distance between any two of the eight sites; different groups occassionally have obtained different numbers, but after discussion, they have arrived at a common answer.

use cooperative group work to generate problem-solving strategies.

freely exchange ideas and participate in discussions requiring higher-order thinking.

collect and organize data needed to solve the problem.

Ms. Ramirez selects a sample route for the walking tour and through discussion with the class explains how the total length of the walking tour is obtained from the matrix of information that the students generated - you find the distances between consecutive sites on the tour, and then add up the walking distances along the tour. She now asks her students to work in groups to decide on a strategy that they think will produce an efficient route (which starts and ends at the parking lot), and to assist the group's recorder in writing a short paragraph explaining their strategy. Some groups decide to list all possible routes and calculate how long a walk each route entails. (Ms. Ramirez asks the students how many possible routes do they think they will have to list.) Other groups suggest that the best route is obtained by always going to the nearest site.

recognize there are numerous ways to solve the problem.

work in cooperative groups to develop alternative strategies.

Ms. Ramirez now asks the students to use calculators to carry out their strategy and determine the travel time for the routes they will be considering. After each group presents its results, the class will together compare the various methods that were proposed and the accompanying results. Among the questions which Ms. Ramirez will ask are: "Do the various methods give the same result?", "Which methods result in a most efficient route?", "What other strategies could we have used?" Responses from the students might include: "always use the shortest distance", "never use the longest distance", "put distances in increasing order and use only those that neither make a loop or put a third edge into a vertex."

compare the variety of strategies proposed.

As a regular feature in his class, Mr. Arbeiter has parents of each student make a presentation about their job and how the various educational disciplines are needed for them to be successful. Today, Emily has asked her Mom, the owner of a heating and air conditioning company, to talk to her class. Mrs. Flinn and Mr. Arbeiter decide to have the students help her solve a problem similar to one which her company faces regularly. She briefly describes her company, the work that she does, and tells the students that they are going to help her determine how large an air conditioner will be needed in the classroom. She poses the following problem: What information about the room would be most important in determining how large an air conditioner is needed? The students quickly agree that the amount of air conditioning would depend on the amount of air in the room, and that in turn, depended on how much space there was in the room. Through suggestions and hints, Mrs. Flinn had them realize that the amount of sunlight entering the room would have an effect as well and they quickly agreed that the area of the windows must be found too.

The students:

interact with parents who use mathematics and other disciplines in their daily lives.

have the time to explore a problem situation thoroughly.

Mr. Arbeiter reminded the class that there is a mathematical term which represents the amount of space, and asked each student to write down that term. As was his custom, Mr. Arbeiter asked six students, one quarter of the class, to read the words they had each written. Four read the word "volume" and two read "area." By a show of hands, he found that about one third of the class had written "area" and two thirds had written "volume." In their groups, the students were asked to discuss the difference between area and volume and to write down the differences between them. As the groups discussed these concepts Mrs. Flinn and Mr. Arbeiter circulated among them, making sure that each group had focused on the difference between area and volume; subsequently the groups read the statements they had prepared, and the entire class discussed and commented on the groups' statements. Mrs. Flinn had the class discuss which of the concepts were needed on the two phases; amount of space in the classroom and how much window space there was.

are regularly assessed through a variety of methods.

work in a variety of settings to develop concepts and understanding.

Now that all students agreed on the difference between area and volume and where each applied in this case, the discussion turned to discussion centered on how one obtains the volume of the classroom and the area of the windows. Although familiar with the concept of volume, the class was not able to calculate volume easily, so Mr. Arbeiter suggested that each group build a rectanguar box out of cubes and figure out how many cubes the box contained. Most groups discovered that they could get the answer by multiplying the number of cubes in the bottom layer by the number of layers (the "height"), and agreed with Mr. Arbeiter's conclusion that V = BxH. When Mr. Arbeiter asked them how they calculate the number of cubes in the bottom layer, all agreed that you multiplied length times width; and when the teacher wrote V=BxH=(LxW)xH, several other groups recognized that that was how they found the volume of their box.

Mr. Arbeiter asked the class "How does the volume formula help us find the volume of the classroom?" The students agreed that the shape of the classroom was about the shape of a rectangular box, but were quick to point out that to any answer obtained by the formula would have to be considered an estimate, since it would not be taking alcoves and pillars into consideration. They agreed to change the question to "How does this formula help us estimate the volume of the classroom?"

use concrete materials to develop a model for volume.

"All we have to do is measure the three quantities - length, width, and height, the three dimensions of the classroom, and multiply the three numbers together" was the prevailing sentiment. Marcia observed that "since we're only going to get an estimate anyway, why should we measure those three amounts exactly?" And Mrs. Flinn noted that her sales people often estimated the size of the room without making any measurements. "How can we estimate the dimensions of a room without makingmeasurements?", she asked. Paula suggested that "maybe the salesperson estimates the three dimensions and multiplies those estimates together." "A great suggestion," Mrs. Flinn responded. "Let's try that ourselves."

recognize and apply estimating to geometric situations.

are exposed to a variety of open-ended questions and respond .

"Let's first estimate the width of the room. About how many inches wide is this room?" Brian pointed out that inches is an appropriate unit for a piece of paper, but not for a room. After a brief discussion, Mrs. Flinn revised her question to "About how many feet wide is this room?"

feel comfortable identifying errors.

The students wrote down their estimates and explanations of how they arrived at them. After hearing all of the students estimates and reasons, the students were asked to return to their regular groups and decide as groups what they thought the width of the room was. "Well," said Mr. Arbeiter, "you all gave good reasons for your estimates, but now let's see whose estimate was closest. We'll measure the width of the classroom." Great cheers were heard for the groups whose estimate was closest to the actual measurement. The same process was repeated for length, and width as well as estimating the window area of the classroom. Mrs. Flinn pointed out that estimates were getting closer to the actual measurements each time they did it. She then showed the class a formula used to determine the number of BTUs needed for a room in terms of the volume of the room and the area of the windows. The data obtained by the class for the volume and window area was entered in the formula, and a quick calculation gave the number of BTUs needed for the classroom. Mrs. Flinn wrapped up her presentation by making the connection between the size needed, the cost of the purchase, and the regular expense of running the air conditioner. She emphasized that the success of her business rested on the sales people and their ability to estimate the needs well.

communicate their answers and defend their thought processes.

examine the correctness of their results.

Mr. Arbeiter thanked Mrs. Flinn for her presentation and asked the students how they would like to practice the skills they had discussed today. Feeling confident, the students volunteered to estimate the data for their other classrooms. Mr. Arbeiter agreed to display the results, so long as the students agreed to leave off estimating while their other classes were in session.

extend their skills through practice in similar problems.

"It isn't fair!", Jasmine announced to her class one Monday morning. "I used up $10 worth of quarters playing a boardwalk game over the weekend at the shore, and I only won once. And all I got for winning was a lousy stuffed animal!"

Ms. Buffon often told her class that mathematics was all around them, and had encouraged them to see the world with the eyes of a mathematician. So she wasn't surprised that Jasmine shared this incident with the class.

"Please explain why you thought there was mathematics here," Ms. Buffon asked Jasmine.

The students:

recognize the role that mathematics can play in explaining and describing the world around them.

"Well, first of all, I threw the quarters onto a platform which was covered with squares, you know, like a tile floor, so that reminded me of geometry. And as I was throwing my quarters away, one after another, I was reminded of all the probability experiments that we did last year, you know, throwing coins and dice. It wasn't exactly the same, but it was like the same."

"Those were very good observations, Jasmine," said Ms. Buffon, "you recognized that the situation involved both geometry and probability, but you didn't tell the class what you had to do to win the game."

connect previously learned mathematics to the current situation.

"Oh, you just had to throw the quarter so that it didn't touch any of the lines!" Ms. Buffon asked Jasmine to go to the board to draw a picture, explaining to her that not everyone will visualize easily the game she was talking about.

use different forms of communication to define a problem and share their insights.

Every other Monday, Ms. Buffon began her geometry class with a sharing session. Sometimes the "mathematics situations" that the students shared did not lead to extended discussions, in which case Ms. Buffon continued with the lesson she had prepared. But she was prepared to use the entire period for the discussion, and even carry it over into subsequent days, if the students got interested in the topic.

are afforded the opportunity to fully explore and resolve mathematical problems.

"Why didn't you think the game was fair?" she asked Jasmine. Jasmine repeated what she had said earlier, that she should have won more often and that the prizes should have been better. Other students in the class were asked to respond to the question, and after a lively interchange, they decided that for the game to be really fair, you should get about $10 in prizes if you play $10 in quarters; but, considering that they were having fun playing the game, and considering that the people running the game should get a profit, they would be satisfied with about $5 in prizes. Jasmine listened to the conversation intently, and chimed in at the end "That lousy bear wasn't worth more than a dollar or two!"

Moving the discussion in another direction, Ms. Buffon said "Now that we understand that it is possible to explain 'fairness' mathematically, let us investigate Jasmine's game to see if it really was unfair. What do you think were Jasmine's chances of winning a prize?"

explore questions of fairness, geometry, and probability.

This question evoked many responses from the class, and after some discussion the class agreed with Rob's comment that it all depended on the size of the squares. Jasmine did not know the actual size of the squares, so the class agreed that they might as well try to figure out the answer for different size squares. Dalia pointed out that this looked like another example of a function, and Ms. Buffon commended her for making this connection to other topics they had been discussing.

are encouraged to make connections to other topics within mathematics.

Returning to her previous question, Ms. Buffon suggested that the students do some experiments at home to help determine the probability of winning a prize. Each pair of students was asked to draw a grid on poster board, throw a quarter onto the poster board 100 times, and record the number of times the quarter was entirely within the lines; to simplify the problem, quarters that landed off the grid were not counted at all. Different students chose different size grids, ranging from 1.5" to 3.5", at quarter inch intervals.

After school, Ms. Buffon visited the Math Lab where she spent some time trying to find materials related to this problem. When she looked under "probability" in the indexes of various mathematics education journals, she was led to several articles discussing geometric probability, which she learned is a branch of mathematics which addresses problems like Jasmine's game. With these resources available to her, Ms. Buffon no longer feels that she has to have all the answers, and can entertain discussions about mathematical topics with which she is unfamiliar. Tomorrow she will be able to tell the class what she has learned!

model problems and conduct experiments to help them solve problems.

The next day the students reported on their results, and Ms. Buffon tabulated them in the following chart, and, at the same time, plotted their results on a graph:

"Do you see any patterns here?", Ms. Buffon asked the class. They all agreed that, as expected, the larger the size of the squares, the more frequently Jasmine would have won the game. "What do you think the size of the squares were on the boardwalk game?" Ms. Buffon asked next. Everyone agreed that the squares were most likely smaller than

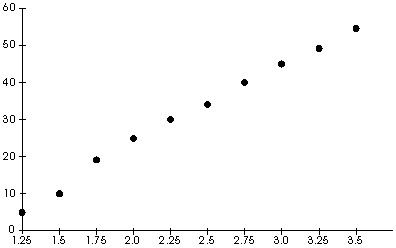
1.25" since her one prize out of forty quarters corresponded to 2.5 wins out of a 100 games, which was lower than obtained for the smallest squares in the experiment. Turning to the graph, Ms. Buffonasked "What would have happened if we tried the experiment with squares smaller than 1.25?" The students laughed, one after another, as they realized that if the size of the squares were small enough, you would never win the game. "Well, then, what would have happened if we tried the experiment with larger and larger squares?" Looking at the graph, the class found this a difficult question, but Fran broke the group's mindset by saying "Yeah, suppose the squares were as big as this room?" Then everyone realized that if the squares were larger and larger, you would become almost certain to win the game. 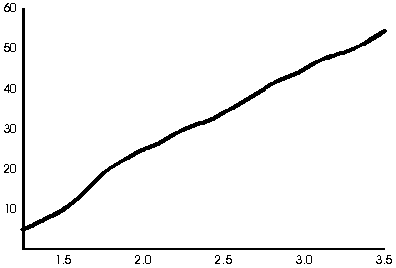"Dalia, do you remember your comment yesterday, that it sounded like we were working on a function?" Ms. Buffon asked. "Would you sketch the graph of that function for the class?" Ms. Buffon made a mental note to discuss this problem with her precalculus students, since she had many questions to ask them about this graph.

collect, analyze, and make inferences from data.

recognize connections between numerical patterns and functions.

"Well, we've gotten a lot of information by using experimental methods about Jasmine's game; let's see if we can figure out the probability theory behind it as well." At this point, Ms. Buffon was eager to tell her class what she had learned at the Math Lab. However, being aware that the students will grasp the solution method better if they have an opportunity to discover it for themselves, she asked the class to discuss the following question in their study groups: "How can you tell from the position of the quarter whether or not you would win the game?" Going from group to group, Ms. Buffon listens to the discussions. When the groups have discovered that to win the game, the center of the quarter must be sufficiently far from the closest border, she gives the groups their next task - to describe where in the square the center of the quarter must be.

formulate and test mathematical conjectures.

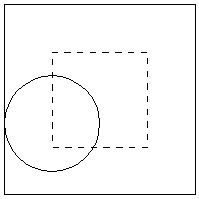
By reasoning in different ways, the groups all arrived at the same picture involving a smaller square inside the original square, and at the same conclusion - that you win if the center of the quarter lies inside the smaller square. With this information, the students are able to calculate the probability for any particular size of the square, and even to write an equation for the function whose graph they sketched earlier.

Having found the probability of winning the game, Ms. Buffon planned to return to the question that began this whole discussion - whether Jasmine's game was fair. But that was the topic for another day.

Note: Ms. Buffon realized that the graph of the function was not linear, as depicted earlier, even though the data seemed to indicate linear growth. With her precalculus students, she would have them translate the above situation into the equation y=(x-d)²/x², where d is the diameter of the quarter. Then she would have them graph the function, enabling them to discover that although the graph appears to be linear, in reality it increases at a decreasing pace, and goes asymptotically to the line y = 1.

construct a pictorial model to represent the problem.

Ms. Jackson is teaching her geometry students to use and identify inductive reasoning.

She asks each student to draw a large triangle on their paper. She then asks the students to hold up their triangles so that they can see the wide variety that have been created. The students observe that all the triangles are different.

Ms. Jackson then asks the students to cut out their triangle, to tear off the corners of their triangle and to place the corners together so that they are adjacent. She circulates around the room to be sure everyone is on task, and tells students to record a description of what they see in their notebooks.

The students:

use a variety of types of mathematical reasoning to solve problems.

Ms. Jackson then asks a representative sampling of students to tell the class what they observed after fitting the corners together. The students report that it looks as if the corners form a straight line. Everyone agrees.

Ms. Jackson now asks the students to write a generalization about the angles of ANY triangle based upon the class results of this activity. She asks another representative sampling of students to state their generalizations. The students conclude that the sum of the measures of the angles of ANY triangle is 180 degrees.

She gives the students a definition of inductive reasoning. They recognize that they have used induction to reach their generalization about the angles of a triangle. She then asks them to think about when they have used inductive reasoning in the past and write an example in their notebooks.

are encouraged to form generalizations based on observations they have made.

Volunteers are asked to share their recollections with the rest of the class. Some are funny and some quite poignant. The teacher asks if anyone can see a drawback to inductive reasoning within social as well as mathematical contexts.

The class decides that one drawback is that you can't check all examples - all triangles cannot be checked to see if the angles always add to 180 degrees. Another is that if you check too few examples you might reach an erroneous conclusion. They discuss how this is the reason for much of the racial and gender stereotyping that they encounter. Ms. Jackson asks students to identify counterexamples for racial and gender stereotypes.

are regularly asked to write about their understandings of mathematics and its uses in the real world.

Ms. Jackson then asks the students to do another experiment. They use their compasses to draw 5 circles. On the first circle, the students identify and connect 2 points with a chord. They then state the number of non-overlapping regions into which the circle has been divided. On the second circle, students identify three points and draw all chords connecting these points. Once again, they state the number of non-overlapping regions into which the circle has been divided. They continue this procedure until they find the number of non-overlapping regions formed when 5 points on the circle are fully connected by chords. Students record their data in a table and use inductive reasoning to predict the number of non-overlapping regions produced by fully connecting n points on the circle with chords:

They are asked to state their conclusion in narrative form.

generate a set of data and use pattern-based thinking to formulate solutions.

The students agree that the number of non-overlapping regions produced by fully connecting n points on a circle with chords is 2^(n-1). Students then test their conclusion by carrying out the experiment with 6 points. Many find their conclusion is wrong for n=6. They fully expected to find 32 regions but only got 31!

As class draws to a close, Ms. Jackson gives a homework assignment in which students will induce as well as produce counterexamples to conclusions. Students leave class somewhat dazed by the last experiment. Many of them tell Ms. Jackson that something must be wrong because they are sure the answer is 32. They tell her that they will prove her wrong by reenacting the experiment at home. She looks delighted and encourages their pursuit.

validate conclusions by looking for counterexamples.

Mr. Miller wants his ninth grade mathematics class to review the rectangular coordinate system, reinforce how mathematics is used to model situations, and develop the concept of exponential functions. He decides this would be an excellent opportunity to utilize a real-world situation. He elects to build his effort around an experiment involving mold growth found in an old SMSG book entitled Mathematics and Living Things.

At the beginning of the unit, Mr. Miller presents the class with a packet of required readings, each of which deals with growth patterns of living things. There is an article on the rabbit population of Australia, another on world population, and another on the spread of AIDS. He explains the goals of the unit, gives the expectations for the readings, and describes the purpose of the experiment the class will conduct. Mr. Miller has students distribute the lab directions and materials, and he has them prepare the medium for the mold growth.

The students:

incorporate scientific applications in their study of mathematics.

On each day over the next two weeks, students record an estimate of the area covered by the mold, the increase in the area from the previous day, and the percent of increase. On Fridays, they are asked to extrapolate the growth they expect to occur on Saturday and Sunday and then interpolate the same information from the growth they see on Monday. They are required to maintain a graph of the percent of increase versus the days. The extrapolated and interpolated points are both graphed with special marks such as "X" or "O."

estimate area of irregular figures.

collect and analyze data.

During the period of data-gathering, Mr. Miller develops

exponential growth through the concept of compound interest and uses a graphing calculator to illustrate the graph of such growth. Each student is asked to suggest a function which would yield something close to their data, and has the opportunity to put their function into the graphing calculator and revise it until they are satisfied with the estimate. Time is provided to have the students discuss their reactions to the readings.

use technology as a tool of learning.

spend the time needed for mathematical discovery.

At the end of the two-week period, Mr. Miller has the students prepare a report relating the graph of their observations to the discussions of the readings and the work on compound interest. To extend the ideas developed in this experiment, students are given different data sets which came from actualmeasurements of various types of growth. Students work in groups, each group taking one of the sets of data. The groups are expected to make a presentation discussing the exponential function which models the growth, what limiting factors could be involved, and the carrying capacity of the environment.

write about their understandings of the connections between mathematics and physical phenomena.

extend their understanding of mathematical concepts through cooperative work and presentation.

As a closing activity, students are asked to choose a country from around the world, examine population growth over some period of time, and write a paper for inclusion in their portfolio discussing the mathematical issues and biological issues involved as well as a general discussion of the impact of such growth on the history of that period.

are assessed through alternative means.

explore the uses of mathematics in other disciplines.