LEARNING ENVIRONMENT STANDARD 17
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| All students' mathematical learning will embody the concept that engagement in mathematics is essential, and that decision-making, risk-taking, cooperative work, perseverance, self-assessment, and self-confidence are frequently keys to success. |
(This "learning environment standard" was developed and approved by the task force that prepared the Mathematics Standards and appears in the Introduction to the Mathematics Standards chapter of the New Jersey State Department of Education's Core Curriculum Content Standards; however, since it was not considered a "content standard", it was not presented to the New Jersey State Board of Education for adoption.)
Descriptive Statement
Engagement in mathematics should be expected of all students, and the learning environment should be one where students are actively involved in doing mathematics. Challenging problems should be posed and students should be expected to work on them individually and in groups, sometimes for extended periods of time, and sometimes on unfamiliar topics. They should be encouraged to develop traits and strategies - such as perseverance, cooperative work skills, self-assessment, self-confidence, decision-making, and risk-taking - which will be key to their success in mathematics.
Meaning and Importance
New Jersey's Mathematics Standards describe what a high-quality mathematics education should comprise for all of New Jersey's students, from kindergarten to 12th grade. Central to these standards is the development of mathematical power for all students, including the ability to explore, conjecture, and reason logically; to solve nonroutine problems; to communicate about and through mathematics; and to connect ideas within mathematics and between mathematics and other intellectual activity. Mathematical power also includes the development of personal self-confidence and a disposition to seek, evaluate, and use quantitative and spatial information in solving problems and in making decisions. Students' flexibility, perseverance, interest, curiosity, and inventiveness also affect the realization of mathematical power.
Keys to Success
Standard 17 discusses the "keys to success" in mathematics, and what teachers can do to make it more likely that each student will acquire these keys.
The keys to success are enumerated in this chapter as cumulative progress indicators, as with other standards, and for each key to success, specific suggestions are provided for how it may be achieved. The first three of these indicators address the student's orientation toward mathematics, and the remaining five indicators address the nature of the student's engagement in mathematical activity.
The other sections of this chapter discuss the learning environment that will facilitate students' achieving this standard. The main sections of this chapter, following this section on Keys to Success, are entitled Organizing the Classroom, Organizing Instruction, and Organizing the Content.
Experiences will be such that all students:
1. Demonstrate confidence as mathematical thinkers, believing that they can learn mathematics and can achieve high standards in mathematics, and accepting responsibility for their own learning of mathematics.
New Jersey's Mathematics Standards are based on the assumption, discussed in detail in Standard 16, that all students can succeed in mathematics. Students need to develop confidence in their own mathematical abilities and performance; they need to recognize that they can understand and do mathematics, and believe that they will succeed in achieving the high standards now expected of them. They need to recognize that success in mathematics, as in other areas, is the result of persistence and hard work.
To help all students achieve mathematical self-confidence, teachers should;
- believe themselves that all students can learn mathematics, even when their students are experiencing difficulties.
- set high expectations for all students, expect students to take responsibility for their own learning, and provide the increased support necessary to help students meet these higher standards.
- build self-confidence in each student by making mathematics understandable, using effective and meaningful teaching methods, relating past learning to concepts currently being taught, establishing short-term, obtainable goals, and providing mathematical experiences at which students can succeed.
- help students make appropriate attributions about effort, persistence, and strategy; student "failures" are often due to the choice of an incorrect strategy or to a lack of effort or persistence, rather than to a lack of ability.
- convey to students that their effort and persistence are critical to their success, and will lead to their success. And our efforts to do this must also be persistent and creative. While NewJersey's Mathematics Standards asserts that all students can succeed in mathematics, all the recommended changes in curriculum, instruction, and assessment will have little impact on students who are unwilling to make the effort.
2. Recognize the power that comes from understanding and doing mathematics.
Students need to realize that by developing their ability to do mathematics, they will be able to understand, formulate, and solve problems in a wide variety of situations. This is because mathematical tools and perspectives are often the key to understanding and solving a problem, even if at first glance mathematics doesn't even appear to be involved. The better they understand and can do mathematics, the greater will be the variety of problems they can solve. As a result, a greater variety of school and career options will be open to them.
To help students recognize the power of mathematics, teachers should;
- provide students with worthwhile mathematical tasks. Such tasks are inherently interesting to students, helping them to develop mathematical concepts and skills, and drawing on their own experiences. They stimulate students to connect mathematics to itself and to other subjects, they encourage students to communicate about mathematics, and they help to develop the students' dispositions to do mathematics. Worthwhile mathematical tasks help students develop a coherent framework for mathematical ideas and present mathematics as an ongoing human activity (NCTM Professional Standards for Teaching Mathematics).
- introduce a variety of activities since different students make mathematics their own in different ways; some students learn best by constructing actual models, others learn best by hearing someone else talk about a mathematical idea, still others learn best by writing down the mathematical concepts for themselves or explaining them to others.
- arrange the journey for the students through the world of mathematics, filling the journey with rich, important experiences which will allow the students to achieve mathematical power.
3. Develop and maintain a positive disposition to mathematics and to mathematical activity.
Students begin school with great interest in solving puzzles and problems, and an enthusiasm for measuring and counting. Over the next few years, many come to believe that mathematics consists of rules which are unintelligible to them, and that math class means rote problems which are not connected to their reality. It is important to convey to students that mathematics is a dynamic human activity to which they can relate.
To help students develop a positive disposition to mathematics and to mathematical activity, teachers should;
- convey their own enthusiasm for and enjoyment of mathematics and solving mathematical problems.
- model persistence, confidence, self-reliance, flexibility, curiosity, inventiveness, and enthusiasm during problem solving, and many students will imitate those traits.
- structure their lessons so that students have fun doing mathematics; of course, this should not diminish the message that learning mathematics is often hard work and is not always exciting.
- make mathematics meaningful through the use of concrete models and discovery lessons.
- demonstrate the usefulness of mathematics in everyday life and relate mathematics frequently to careers. This is extremely important in the middle grades and high school, as students begin to make choices about their futures.
- consider students' interests when planning instruction; field trips, guest speakers, and videos may help spark interest and communicate the ever-present nature of mathematics.
- promote students' intrinsic motivation to learn mathematics by stimulating their curiosity, and provide students with choices and some control over the learning environment, especially in the middle and secondary grades.
- recognize that students have different learning styles and address those different learning styles regularly to ensure that all students remain engaged with mathematics.
- recognize that some students will take more time than others to develop their understanding of a specific topic. Teachers should ensure that students who are proceeding more slowly than their classmates receive the additional support they need and do not become discouraged.
4. Participate actively in mathematical activity and discussion, freely exchanging ideas and problem-solving strategies with their classmates and teachers, and taking intellectual risks and defending positions without fear of being incorrect.
Students should be actively involved in the learning of mathematics. Although some students absorb mathematics through teacher presentations, all students learn better when they are actively engaged in the learning process. Students need to be active participants in their mathematics classes, discussing mathematics with the teacher and with each other, engaged in activities which enhance their learning. They need to be prepared to propose strategies for solving problems, to provide explanations for why things work as they do, and to make conjectures for the consideration of their classmates. In order for them to do this, they must have a supportive classroom environment which encourages diversity of thought.
Teachers should establish this supportive classroom environment by;
- making mathematical discussions a daily activity.
- encouraging students to make suggestions and conjectures, and to propose strategies and explanations.
- conveying to all students that they must all listen to their classmates respectfully and respond to their suggestions as members of a learning community. Students are often reluctant to speak about mathematics unless they are sure of their answers. They need to feel that their incorrect answers will be respected and are part of the learning process; they need to be sure that their answers will not simply be rejected and that they will not be humiliated. The teachersets the tone of the classroom by ensuring that all who speak will be treated respectfully and their suggestions will be taken seriously.
- encourage students to take intellectual risks, and convey that everyone can learn from their mistakes.
- lead students from a partial to a complete solution through asking a question or through posing a new problem that offers an opportunity to think about evidence not previously considered. It is crucial that teachers go beyond simply rejecting a response or pointing out the student's error.
5. Work cooperatively with other students on mathematical activities, actively sharing, listening, and reflecting during group discussions, and giving and receiving constructive criticism.
Students should see themselves as participants in a learning community, where students learn from each other as well as from the teacher and print and electronic materials. While it is sometimes difficult for each student to participate in a whole-class discussion, when students work in groups on mathematical tasks, they can all be active participants, each sharing in the discussion. They also need to listen to and reflect on what other students are saying, so that they can learn from each other's approaches and insights. They need to complete their objective, whether it is a common understanding of a situation or a common solution to a problem, without diminishing each other's unsuccessful attempts along the way.
To help develop students' abilities to work cooperatively with other students, teachers should;
- create regular opportunities for students to work in groups on mathematical tasks, which may include quiet reflective time, so that all students have an opportunity to articulate their understanding of a concept and their strategy for solving a problem.
- structure the group activity so that all students participate appropriately - sharing in the discussion, listening to each other, responding to each other's suggestions with respect, and reflecting on each other's suggestions for completing the task.
- ensure that all students are provided with ample time to think through a problem situation before moving on to its solution.
- teach mathematical ideas, whenever possible, through posing a problem, setting up a situation, or asking a question. Resist the impulse to give an answer or an explanation when a student is confused; try to provide the student with an opportunity to think in a different way about the situation, for example, by asking a related question or posing a different problem which may help them find a solution to the original problem.
- spend more time on a few rich activities rather than a little time on a lot of different ones. Similarly, cover a smaller number of topics well rather than many different topics superficially.
6. Make conjectures, pose their own problems, and devise their own approaches to problem solving.
As noted in the First Four Standards, posing and solving problems is an important cornerstone of New Jersey's Mathematics Standards. Students should be encouraged to become mathematically active, looking for mathematics in the world around them, formulating mathematical questions, and engaged in answering those questions. They need to understand that problem solving means being able to solve problems to which routine methods may not apply, so that they may need to be creative in choosing problem-solving strategies.
To encourage their students to be mathematically active, teachers should;
- encourage their students to explore the world of mathematics and mathematics in the world by asking questions themselves and by encouraging their students to ask questions.
- present the students with problems that they don't already know how to solve, and encourage them to make conjectures about what the solution might be and how it might be obtained.
- encourage students to generate other problems suggested by a problem that has just been solved.
- recognize that there are often many paths to a solution, and should encourage students to develop their own solutions when appropriate.
- model that errors happen in the course of solving problems, and that what is important is how one gains information and recovers from one's errors.
- understand that posing non-routine problems provokes emotional issues from students who are experiencing cognitive difficulties with the subject matter, and find ways of discussing and dealing with affective issues that arise in the context of problem solving (DeBellis, 1996).
7. Assess their work to determine the effectiveness of their strategies, make decisions about alternate strategies to pursue, and persevere in developing and applying strategies for solving a problem in situations where the method and path to the solution are not at first apparent.
Students need to be able to reflect regularly on their mathematical activity and determine whether they are making appropriate progress toward solving a problem. Just as a carpenter makes decisions about which tools to use, the problem solver needs to reflect regularly on whether the right tool is being used. If a problem-solving strategy is not successful, the student may need to try another strategy, although it is possible that later she will discover that the original strategy was after all appropriate.
To encourage students to assess their problem-solving efforts, teachers should;
- encourage their students to step back regularly from their problem solving activity, articulate the strategy that they are currently pursuing, reflect on whether their efforts seem fruitful, and, if appropriate, formulate other options and make the decision to alter their strategy. As in other areas, teachers need to model this behavior, occasionally stepping back and reflectingon whether the whole class activity is moving toward a solution of the problem, and if not what alternate strategy should be adopted.
- encourage students to persevere if they are moving in the right direction, since they tend to give up too easily, particularly if the problem is one which can't be solved in a short time.
8. Assess their work to determine the correctness of their results, based on their own reasoning, rather than relying solely on external authorities.
Students need to develop self-confidence not only in their mathematical abilities, but also in their mathematical performance. If they understand a problem, develop a strategy for solving it, and then obtain an answer, they need to be able to conclude, with some measure of certainty, whether or not they have done the problem correctly. An answer supplied by the teacher, or by an answer key, should provide confirmation of what they already have shown to be the case.
To help students become more willing to assess their own work, teachers should;
- encourage students regularly to validate their own work rather than depending on someone else to tell them whether they are right or wrong; when students request the answer to a problem, teachers should ask them first to explain how they arrived at their answer, whether they believe it to be correct or incorrect, and why. Through this process, if they are correct, they should be able to accept the validity of their reasoning. If they are incorrect, they may be able to correct their errors; alternatively, the teacher will pose a question which will enable them to reconsider and revise their solution.
- encourage students to use each other as sounding boards; students can often find their errors or validate their claims through such discussions.
- take note that in some cases students who exhibit inappropriate self-confidence in their mathematical understandings; in such cases, teachers must ensure that their self-confidence does not interfere with their critical analysis (DeBellis, 1996).
The Professional Standards for Teaching Mathematics (NCTM), suggests that we shift:
|
||||||||||||||||||||||||||||||||||||
Students will develop positive attitudes toward mathematics when they are taught good mathematics in a supportive, enabling environment, when all students' mathematical learning embodies the notion that engagement in mathematics is essential and that where decision-making, risk-taking, cooperative work, perseverance, self-assessment, and self-confidence are frequently keys to success.
|
I Love Math! On Valentine's Day (or as close to that day as the calendar allows), the math department at Lower Cape May Regional School District has "I Love Math" Day. This is a day when students express their love of mathematics in many different ways: writing songs, making posters, making buttons or other "jewelry" to wear, baking cakes and decorating them with math terms and symbols. The students earn extra-credit points and must display their love of math all day. One teacher did not have his students participate and waited until the following day and had his own "I Love Math Even More" Day. |
Organizing the Classroom
The Physical Environment
The physical environment of the classroom is an important consideration in planning for effective instruction. The vision for mathematics in our schools calls for students who are excited by and interested in their activities, who work together to find solutions to real problems, who use technology and other tools as an integral part of the process, and whose learning is conceptually-based, meaningful, and connected to previous mathematics learning and to the real world. The standards call for students who accept responsibility for their own learning, using time effectively and efficiently in order to further their understanding of mathematics.
The physical environment of the classroom must be congruent with the vision we have for our schools. The organization of the classroom should foster a spirit of discovery. Technology and other tools, such as manipulatives, need to be readily and easily accessible to all students. Teachers need collections of supplementary materials to serve as resources. All students should have calculators appropriate to their grade level, and each classroom should have at least one computer and software available at all times for both teacher demonstration and student use. Additional computers should be available for use by the class as a whole. An overhead projector and screen should be available at all times, and teachers should have easy access to other audiovisual equipment as needed.
The classroom itself should be a pleasant place. It should be cheerful, bright, well-lit, and attractive. It should be furnished with flat-top desks or tables and chairs; these can be easily rearranged to accommodate different sized groups and work well with manipulatives, calculators, and printed materials. While each teacher will want to develop a semipermanent room arrangement that conforms to his/her dominant form of instruction, the room should provide sufficient flexibility to rearrange the furniture for different types of activities. Ample space for movement is essential, as is convenient storage space for supplementary resources, manipulatives, supplies, calculators, and computers. Classrooms must also be equipped with adequate electrical power and communications capabilities. Classrooms for younger children should have "messy" areas where children can use water, paint, or sand.
In developing an arrangement of the classroom, the teacher must consider several factors. "How will an arrangement affect my ability to move around the room, checking on student progress?" "Will this arrangement help my students to feel involved in the class activities?" "Will I be able to use small groups as well as have individual work, pairs, and whole class activities?" Some teachers like to organize student desks into groups of four (e.g., Marilyn Burns), while others like to have student desks grouped in pairs, facing the front of the room. Still other teachers prefer a U-shaped arrangement two rows deep (e.g., David Johnson).
The classroom envisioned in New Jersey's Mathematics Standards is not a quiet place. It is a place in which students are excited about learning mathematics, in which they work together purposefully to accomplish a task, in which they talk and make noise and sometimes even jump for joy!
Classroom Routines
Planning effective routines for beginning class, checking and discussing homework, taking roll, collecting and distributing papers, and handling make-up work can save valuable class time and minimize disruptions.
It is important to teach students classroom rules and procedures as they are needed, with special emphasis on this area in the first weeks of school. Many teachers have found that it is helpful to have students rehearse procedures. Others use incentive systems to help shape student behavior. Still others coach students to respond to specific signals, such as the teacher's raising her hand for silence or turning down the lights. Students also need to be taught how to follow directions, how to copy assignments from the board, how to find pages in their text, how to take notes, and how to prepare for tests and quizzes.
Beginning the Class. The first five minutes of a class are the most important. They set the tone for the class and the pace for the entire class period. It is important for students to spend this time productively, rather than in waiting for the teacher to complete clerical tasks. Some possible ways to start a class include the following.
 |
SUGGESTIONS |
 Give students a do-now or warm-up problem. It may be a review
problem, a puzzle, a quiz, a question relating to the new lesson, or a
problem similar to the ones done for homework. At the elementary
level, this is sometimes referred to as five-minute math.
Give students a do-now or warm-up problem. It may be a review
problem, a puzzle, a quiz, a question relating to the new lesson, or a
problem similar to the ones done for homework. At the elementary
level, this is sometimes referred to as five-minute math.
 Have some students do problems related to their homework at the
board, while the others do the same problems at their seats. Spend no
more than five minutes in this activity.
Have some students do problems related to their homework at the
board, while the others do the same problems at their seats. Spend no
more than five minutes in this activity.
 Start each class with mental computation activities or a drill on
mathematical facts.
Start each class with mental computation activities or a drill on
mathematical facts.
|
Calendar Math Mr. Haynes starts his second-grade class each day by asking students to name the day of the week and then write a sentence that states the day of the week and the date. "Today is Monday, September 8th, 19--." He asks them questions such as "What day of the week will it be two days from now?" or "What will the date be in two weeks?" He also has the students keep track of the number of days they have been in school in two different ways: by writing the number on a long roll of adding machine tape and by adding one craft stick to bins marked for ones, tens, and hundreds. The weather symbols that are put on the calendar are used at the end of the month for data analysis activities. Temperature is read from a thermometer and posted on the calendar. Special events are posted on a sheet near the calendar, with the date at the top of the page. These sheets are saved and used later for sequencing, calendar, and data analysis activities. |
 There are frequently other spots during the class period or, in
the elementary grades, during the day, when a short span of time is
available for students to complete a brief task. Teachers need to
plan sponge activities to absorb productively these
short gaps: questions to think about, mental math, estimation, or
problems to solve. Such activities are sometimes called minute
math.
There are frequently other spots during the class period or, in
the elementary grades, during the day, when a short span of time is
available for students to complete a brief task. Teachers need to
plan sponge activities to absorb productively these
short gaps: questions to think about, mental math, estimation, or
problems to solve. Such activities are sometimes called minute
math.
Organizing Distribution of Materials. In order to minimize the time spent setting up, distributing, or gathering equipment, supplies, or materials, it pays to plan ahead. Teachers should have everything set up in advance, if at all possible. Much time is wasted if teachers have to move from one room to another between periods.
 |
SUGGESTIONS |
 Take roll by using a seating chart and noting which seats are
empty or while checking to see who completed their homework. Remember
that, while this should be done early in the period, it does not have
to be the very first thing. Take roll while students are working.
Take roll by using a seating chart and noting which seats are
empty or while checking to see who completed their homework. Remember
that, while this should be done early in the period, it does not have
to be the very first thing. Take roll while students are working.
 Designate one person from each group (if students are working in
groups) to distribute materials, another to collect materials, and a
third to distribute and collect papers.
Designate one person from each group (if students are working in
groups) to distribute materials, another to collect materials, and a
third to distribute and collect papers.
 To help students who have been absent, teachers have devised a
number of strategies which minimize class disruptions. Some
teachers post assignments on the bulletin board in a central
location. Others keep a notebook of assignments throughout the year.
Still others give carbon paper to a student in the class, asking them
to make a copy of their notes for absent students.
To help students who have been absent, teachers have devised a
number of strategies which minimize class disruptions. Some
teachers post assignments on the bulletin board in a central
location. Others keep a notebook of assignments throughout the year.
Still others give carbon paper to a student in the class, asking them
to make a copy of their notes for absent students.
 Organize manipulatives in order to reduce time lost in
distributing and collecting them. Some teachers, especially those in
the primary grades, prefer to have manipulatives set up in learning
centers around the classroom, easily accessible to students working in
small groups. Other teachers prefer to use manipulatives with the
whole class at one time. These teachers find that it is helpful to
package manipulatives in quantities appropriate for the group that
will be using them (individuals, pairs, groups of four or six), using
baggies, boxes, or buckets. Teachers who move from room to room may
find see-through boxes or labeled tote bags, especially those with
zippers, useful for storage of materials.
Organize manipulatives in order to reduce time lost in
distributing and collecting them. Some teachers, especially those in
the primary grades, prefer to have manipulatives set up in learning
centers around the classroom, easily accessible to students working in
small groups. Other teachers prefer to use manipulatives with the
whole class at one time. These teachers find that it is helpful to
package manipulatives in quantities appropriate for the group that
will be using them (individuals, pairs, groups of four or six), using
baggies, boxes, or buckets. Teachers who move from room to room may
find see-through boxes or labeled tote bags, especially those with
zippers, useful for storage of materials.
 Organize calculators for use in the classroom. In some schools,
students are issued calculators individually, like textbooks. In
other schools, students keep calculators in their desks. In still
other schools, teachers keep classroom sets of calculators, which they
distribute for use in class. In any case, it is useful to number the
calculators and assign each student a number, which they will use
throughout the year. Calculator caddies, looking something like
hanging shoe bags, may be purchased to hold the calculators. The
numbered pockets for each calculator make it easy to see which
calculators have been returned.
Organize calculators for use in the classroom. In some schools,
students are issued calculators individually, like textbooks. In
other schools, students keep calculators in their desks. In still
other schools, teachers keep classroom sets of calculators, which they
distribute for use in class. In any case, it is useful to number the
calculators and assign each student a number, which they will use
throughout the year. Calculator caddies, looking something like
hanging shoe bags, may be purchased to hold the calculators. The
numbered pockets for each calculator make it easy to see which
calculators have been returned.
Organizing Homework Review and Collections. Teachers should plan specifically how they will accomplish such tasks as collecting or checking homework.
 |
SUGGESTIONS |
 Try an alternative to calling on students for answers when
homework questions have short answers. Some teachers write the answers
to the homework problems on a transparency, while others write answers
on the board. Some teachers simply read the answers aloud from an
answer key or ask a student to do so. In some classes, it may be
appropriate for students to have answer keys themselves, which they
may use in checking their work as they do it at home.
Try an alternative to calling on students for answers when
homework questions have short answers. Some teachers write the answers
to the homework problems on a transparency, while others write answers
on the board. Some teachers simply read the answers aloud from an
answer key or ask a student to do so. In some classes, it may be
appropriate for students to have answer keys themselves, which they
may use in checking their work as they do it at home.
 Emphasize how students did their homework problems as well as
whether or not they got the right answer. Regardless of the method
chosen to check homework, some time must be spent discussing the
homework. Discussing all of the homework problems, however, is likely
to be a waste of time for many of the students (and will discourage
them from completing it prior to class time!) One technique that some
teachers use is to have students indicate which problems they would
like to discuss on the chalkboard as they enter the room by placing
tally-marks next to the question number. The process of "going
over the homework" can be speeded up by having several students
at the board at one time, each doing a different problem. Students at
their seats may be given a different practice problem to do while
others are writing at the board. Another technique which may be
useful is giving students an opportunity to correct a problem that
they missed prior to discussing the homework.
Emphasize how students did their homework problems as well as
whether or not they got the right answer. Regardless of the method
chosen to check homework, some time must be spent discussing the
homework. Discussing all of the homework problems, however, is likely
to be a waste of time for many of the students (and will discourage
them from completing it prior to class time!) One technique that some
teachers use is to have students indicate which problems they would
like to discuss on the chalkboard as they enter the room by placing
tally-marks next to the question number. The process of "going
over the homework" can be speeded up by having several students
at the board at one time, each doing a different problem. Students at
their seats may be given a different practice problem to do while
others are writing at the board. Another technique which may be
useful is giving students an opportunity to correct a problem that
they missed prior to discussing the homework.
 Motivate students to do their homework. Since homework is
intended to be a learning experience for students, it is generally not
advisable to collect it and grade it for correctness. More beneficial
is checking to see that students have done their homework, either by
moving around the room as students are working or by giving homework
quizzes, such as the one shown below (Johnson, 1982, p. 27).
Motivate students to do their homework. Since homework is
intended to be a learning experience for students, it is generally not
advisable to collect it and grade it for correctness. More beneficial
is checking to see that students have done their homework, either by
moving around the room as students are working or by giving homework
quizzes, such as the one shown below (Johnson, 1982, p. 27).
|
Homework Quiz Directions: Do not open your textbook. Open your notebook to your assignment section. In your homework, find each problem given below. Copy your work for that problem, including all steps and solutions. No credit will be given for just an answer.
1) Feb. 13 - Page 196, problem 6 |
 Have students keep mathematics
notebooks to record homework assignments, vocabulary words, examples
of problems with explanations, and records of group work. Open-notes
quizzes allow students to use their notebooks to find the needed
information and to develop strategies for checking their own work.
Have students keep mathematics
notebooks to record homework assignments, vocabulary words, examples
of problems with explanations, and records of group work. Open-notes
quizzes allow students to use their notebooks to find the needed
information and to develop strategies for checking their own work.
Summary
Clearly teachers need substantial amounts of time, materials, and equipment to create an effective learning environment. More time and access to resources are needed for planning and developing the types of lessons envisioned in the Standards. Schools may need to consider the possibility of having double mathematics periods, extended mathematics classes to provide time for the use of manipulatives and technology, or combined mathematics/science classes. Students also need sufficient time, free of distractions and interruptions, to learn. Scheduling must be guided by the needs of students and what they are expected to learn.
Organizing the classroom appropriately can help teachers to find the time to focus on students' understanding, to build the bridges from the concrete to the abstract, to make the connections between mathematics and the real world, to develop students' problem solving and communication skills, and to help students develop their ability to reason mathematically.
Organizing Instruction
"In reality, no one can teach mathematics. Effective teachers are those who can stimulate students to learn mathematics. Educational research offers compelling evidence that students learn mathematics well only when they construct their own mathematical understanding. To understand what they learn, they must enact for themselves verbs that permeate the mathematics curriculum: 'examine,' 'represent', 'transform,' 'solve,' 'apply,' 'prove,' 'communicate.' This happens most readily when students work in groups, engage in discussion, make presentations, and in other ways take charge of their own learning." (Everybody Counts, 1989, pp. 58-59)
Although it is important that instruction be problem-based, no one instructional strategy can develop the mathematical power that students need. Research findings on learning, on learning styles, and on attitudes all suggest that use of a variety of instructional strategies is most appropriate.
In order to accomplish these expectations, teachers need to use different instructional methods for different purposes. Some of these instructional strategies may involve whole-class, teacher-directed activities, while others may involve students in working in cooperative learning groups. Some instructional strategies may involve discovery learning, with students working in a variety of settings.
Whole-Class, Teacher-Directed Instructional Strategies
Whole-class, teacher-directed instructional strategies may involve the teacher as a "sage on the stage," as in a lecture or demonstration, or as a "guide on the side," as in a discussion or question and answer session. The variety of strategies in this category are illustrated in the vignette on the following page.
|
Vignette - Tangrams
Mr. Hudson began class by asking the students about some of the
games they enjoyed playing on rainy days. He listed each game on the
board and then asked the students to describe the mathematics that
they used in playing that game. After some discussion, he explained
that they would be making an ancient Chinese game in class. He
distributed square pieces of construction paper to each student. He
held up a square and asked the students, "What can you tell me
about this shape?"
Then Mr. Hudson asked the students to put their pieces back together into a square. After each student had completed this task, Mr. Hudson continued to the next fold, again questioning the students about the resulting shapes and asking them to put the pieces back together into the original square. This continued until the students had cut their squares into the seven pieces of the tangram. "Let me tell you about this puzzle," said Mr. Hudson. "Legend has it that this puzzle was invented by a poor Chinese boy as a present for the boy emperor, who loved puzzles. In 1813, a Chinese book about tangrams stated that, 'the origin of the seven-piece puzzle is not known,' suggesting that, even then, the tangram was thought to be very old. However, references prior to 1800 have not been found. There was a lot of interest in China in tangrams around 1800; the puzzle was considered primarily a game for children and women at that time. The puzzle became known about this time in the Western countries. At first, most books on tangrams were translations of Chinese works. Later books were more original. Most noteworthy is The 8th Book of Tan by Sam Lloyd, published in 1913. Lloyd provides much historical documentation regarding tangrams, all of it completely made up, claiming that the puzzle originated with a monumental work in seven volumes, which was compiled in China 4000 years ago. However, at that time, the Chinese were still at the stage of using crude pictographs scratched on turtle shells for writing. The name of the puzzle, tangram, most likely comes from the South Chinese word for 'Chinese,' 'tang,' combined with the common ending `gram.' "The tangram can be used to make more than 300 different designs, including the numerals and the letters of the alphabet. Let me show you how to make an A. Mr. Hudson used tangram pieces on the overhead projector to demonstrate how the pieces could be used to make an A Then he used the pieces to show some different designs, asking for each, "What does this look like to you?" The first design was a boat, the next a candle, and the last a bell. "Tangrams can be used to depict many things, even the story of Cinderella. Today, however, we are going to use them to make some geometric shapes." Mr. Hudson distributed a sheet with several geometric shapes and asked the students to work in pairs to make these shapes out of the tangram pieces. |
In the vignette, Mr. Hudson uses a variety of whole-class, teacher-directed instructional strategies before asking the students to work in pairs on a lab activity. First, he involves the students in a discussion about games that they had played. During discussions, both teacher and student are talking. Generally, discussions are initiated by questions posed by the teacher, although it is also possible to generate a discussion from student-initiated questions. Discussions are useful mechanisms for forcing students to develop their own thoughts about mathematics and to communicate their ideas to others. Some teachers have found that the quality of discussions is enhanced by asking students first to respond briefly in writing to a question before beginning a discussion. Discussions will be more effective if listening is not a passive activity; students should listen to one another, incorporate new ideas into their own thinking, and evaluate their own understanding. Some teachers follow up discussions by asking students to write about what they learned, what they think are the key ideas, or what they do not understand.
Following the discussion, Mr. Hudson involves the students in a question-and-answer session. In this, the teacher poses questions for students. Question-and-answer may be used quite effectively to provide a quick check on student understanding of a concept by asking all students to respond on chalkboards, flip books which they all show the teacher at the same time, or by showing their answers with manipilatives. Although this strategy can be used as a quick check on factual information, not all questions should be single-answer, low-level responses. Questions should also encourage students to explain different ways to find an answer. Some questions should challenge students' thinking, asking them to clarify their answers and justify their thinking. (A practical reference on questioning is David Johnson's book, Every Minute Counts: Making Your Math Class Work.)
Next, Mr. Hudson provided some background information on tangrams by lecturing briefly. Lectures, or teacher talk, are presently the dominant form of instruction in many mathematics classrooms. Lectures are most appropriate for providing factual information for motivated students. They are most effective when they are directly related to the objectives of the lesson, when the teacher uses relevant examples, and when the teacher avoids the use of vague terms. Most lectures are based on the philosophy of filling students' empty minds with factual information; such an approach runs contrary to research findings indicating the importance of involving students actively in processing information and of relating new learning to past learning. A major disadvantage of the lecture strategy is the low level of retention that can generally be expected.
The last whole-class, teacher-directed instructional strategy that Mr. Hudson uses is the teacher demonstration. Mr. Hudson uses the overhead to show the students how tangrams can be used to make several different designs. Another teacher might use a geoboard on the overhead projector to demonstrate the relationship between the area of a right triangle and that of a rectangle. Still another teacher might use models of a cube and a square pyramid with the same base and height to demonstrate the relationship between the volume of a prism and that of a pyramid. Demonstrations are often used in combination with other instructional strategies. Effective classroom demonstrations require clarity, enthusiasm, good questioning techniques, and student involvement (see Prichard & Bingaman, 1993).
Discovery Learning
Discovery learning may take place in a whole-class setting, in small groups, or on an individual basis. In a whole-class setting, it is generally guided by the teacher. In small groups, discovery learning usually involves some type of mathematics lab. Individual discovery learning generally involves student projects. Discovery activities should involve important mathematics, make connections among mathematical topics, link mathematics to other subject areas and to the real world, and include assessment as an integral part of the instructional activity.
Projects
|
Mr. Arnold has assigned individual projects to students in his seventh grade class. One such project is to determine how much postage is wasted on the "junk mail" that arrives at that student's home during a typical month. Barbara has been carefully examining the mail each day when she arrives home, and has been taking careful notes on how much postage appears each day on this junk mail. She then brings the data into class, where she enters it on a graph she has been keeping in her portfolio. She also adds the amount spent on the postage to a running total which she also keeps. When Mr. Arnold asked Barbara what the graph was being used to describe, she informed him that she had noticed that more junk mail seemed to arrive on Tuesdays than on any other day. The graph was being used to determine on which day the most junk mail actually arrived. Although not technically a part of her assigned project, it was something that had occurred to Barbara, she had discussed it with Mr. Arnold, and they had agreed that she should keep a record on a day-by-day basis. |
In this vignette, the students have been working by themselves as much as possible. This technique has permitted the students to determine what techniques they will use to gather the data they need for their project, and to decide what the best method of keeping and presenting this data will be. The projects have been assigned individually, and Mr. Arnold has given them one month to complete their study. Some time has been allotted in class periodically, but most of the work is done at home or during free time.
Mr. Arnold has found that the use of individual work puts the student into the role of the living mathematician. The projects are "real-world" in nature, and show the students some areas in which their mathematics is used outside of class. This independent work provides an opportunity for some statistics, as the students decide what data they want, how they will best collect it, and finally, how they will write up and present their findings to the entire class. Mr. Arnold has been using the projects technique for several years now, and the students seem to enjoy being "living mathematicians," as one student put it.
Mathematics Labs
|
Ms. Horatio has students working in small groups in her first-year algebra class. The students have been given a laboratory sheet that leads them through an activity designed to help them discover trinomial factoring. Using a series of large squares (representing x2), rectangles (dimensions x by 1, representing an area of x), and unit squares (representing units), the students are building a series of rectangles whose areas are expressions such as x2 + 4x + 3 (length = x + 3, width = x + 1); x2 + 5x + 6 (length = x + 3, width = x + 2); etc. After experiencing five or six of the rectangles, the students begin to see the quadratic expressions as areas, and the factors as the length and the width. While the students are working in their groups, Ms. Horatio moves about the classroom helping the students build their rectangles. She occasionally asks a leading question, designed to keep the students "on-track." Once they have demonstrated their ability to "build" the rectangles, Ms. Horatio gathers them into a large group and helps them make the transition to the abstract, in which students are given a quadratic trinomial to factor without using the manipulatives. |
The type of teaching strategy used in the vignette at the left permits the students to make use of a laboratory setting to discover how to factor. The discovery technique permits them to make use of manipulatives until they gain the concept at hand. The discovery technique permits the students to enjoy creating their own mathematics. Using a laboratory setting at this level is somewhat different for her students. One disadvantage which Ms. Horatio faces, however, is the distinct possibility that some students may discover some concepts which differ from those she is attempting to have them learn, or may even be incorrect concepts. She controls these possibilities to some extent by moving about the classroom during the discovery period and "helping" the students with their work. Her lab sheet is somewhat directed, so that students will not move too far from the desired discovery.
Lab activities involving data collection are also becoming more common in the mathematics classroom. Such activities involve doing an experiment, often with some type of equipment, recording data in a suitable form, analyzing the data (looking for patterns and making generalizations), and reporting back the results. Usually these labs are completed by small groups of students working together. Sometimes the lab report is generated as a group; at other times, it may be prepared by each individual in the group.
Whole Class Activities
|
Ms. Lovelace's second-graders are investigating addition by using base ten blocks. Ms. Lovelace begins by pairing up the students. She asks one student in each pair to represent the number 25, using as few blocks as possible, while the other represents the number 28, again using as few blocks as possible. Then she asks the students to combine the blocks and tell her how many there are in all. She asks several pairs to explain how they found the answer and then introduces a method for recording what the students have done with the blocks. |
|
Mrs. White wants her high school class to see how changes in an equation affect the graph of that equation. She believes that the overhead graphing calculator will be the best tool to use to accomplish this. (It's easier to keep everyone looking at the same thing with the overhead than it is with individual graphing calculators, and it's easier to set up the graphing calculator than it is to use the computer.) She begins by graphing the equation y = x2. She asks students to predict how the graph will change if it is changed to y = x2 + 3. She enters this on the graphing calculator and asks the students to describe what happened. She does several more problems involving adding a constant and then asks the students to write down the pattern they have found. She continues the lesson by examining the effects of other constants. |
Both of the examples above illustrate discovery learning in a whole-class, teacher-guided situation. This instructional strategy is frequently used in conjunction with a demonstration and discussion. Keeping all of the students in a single group provides a more consistent experience for all of them but also generally provides fewer opportunities to articulate patterns and describe generalizations than does working in small groups. (Useful references on discovery learning are the books by J. G. Brooks and M. G. Brooks, M. Burns, C. K. Kamii, and D. Chazan and R. Houde listed in the References.)
Cooperative Learning
|
In Mrs. Exton's sixth-grade class, the students have been presented with a task to perform. The following sequence of numbers has been placed on the board: 9, 16, 23, 30, 37, 44, 51, ... Mrs. Exton has placed the students into working groups of four, and each group has been asked to examine the sequence of numbers and tell all they can about the sequence. Mrs. Exton is circulating among the groups, observing the students as they work, and from time to time, making a comment to some of the groups as she passes by. As the groups work, there is a chattering noise throughout the classroom. "The difference is always 7." "The first two numbers are squares. Are there any other squares?" "Take 2 from each number and you get the 7's table." "If we add 5 to each number, we get the 7's table." "Two of the numbers are primes. Are there any more if we go on?" "Look at this pattern that you get if you add up the digits in each number!" In most of the cases, other students within the group answer the questions as the group continues to explore. After about 10 minutes, Mrs. Exton calls the groups to order and has one person from each group present their group's findings. |
In this vignette, we see a classroom of youngsters working in cooperative or collaborative groups. In this case, the teacher has placed the students into the groups, in order to ensure that each group has a wide distribution of abilities and that personal problems are kept to a minimum. All students in the group are encouraged to contribute, answering questions within their own group. Each student is expected to be able to explain what the group did. Mrs. Exton changes the groups every four or five weeks. Her role is to establish the objectives of the lesson, provide the stimulus for discussion, monitor the groups, and to intervene only when absolutely necessary.
Other teachers may organize cooperative learning groups in different ways. Some teachers prefer to let students select their own groups, at least on occasion. Some teachers prefer to change groups more frequently, depending on the activity planned for a particular day. Some teachers prefer to occasionally have students of like abilities and backgrounds working together. Some teachers like to assign roles to individuals in the group: facilitator (keeps the group on task), recorder (writes down ideas), reporter (reports to class), reader (reads problem and checks accuracy of facts), materials handler (gets needed materials). Still another cooperative learning strategy is the Jigsaw method, in which each member of a group is assigned an area to research, all those having the same topic work together to learn about that topic, and then they disperse back to their original groups to teach the rest of their group about that topic. (Useful references on cooperative learning are the books by A. Artzt and C. Newman, and by N. Davidson in the References.)
|
Math Buddies In Janet Pike's sixth-grade math class at Reed Avenue School in Millville, students work in pairs called Math Buddies. Buddies work together in checking homework, correcting homework mistakes, working at the chalkboard, writing in math notebooks, using manipulatives, and calculator activities. They also work on projects and reports as a team. The students look forward to specific days when Math Buddies are required. Not all lessons or daily objectives lend themselves to the "buddy system," but on most days the arrangement allows for maximum involvement, understanding, and exploration. |
It is said that we really learn a concept when we teach it to someone else. Cooperative learning allows for peer teaching-tutoring, actively engaging students in a process which facilitates long-term retention of mathematical concepts. Cooperative learning has also been shown to have a positive effect on student achievement and interpersonal relationships (Slavin, 1990). It improves student attitudes toward racial and ethnic groups. The group often helps to keep low-achieving students on-task. Above all, the group helps keep students more actively involved in the learning process. However, using cooperative groups to the exclusion of any other teaching strategy is as inappropriate as using only lectures.
Summary
A variety of teaching strategies have been described in this section. Individual lessons lend themselves to different styles of teaching. It is the job of the teacher to match the particular strategy of teaching with the topic of the lessons and to utilize as wide a variety of strategies as possible. Using a variety of strategies helps to make the mathematics classroom more interesting to students and to make the subject of mathematics come alive as they learn. The mathematics teacher must plan the most effective strategies to engage students in learning, retaining, and applying important mathematics.
"The most useful metaphor for describing the modern teacher is that of an intellectual coach. At various times this will require that the teacher be
- A role model who demonstrates not just multiple paths to a solution but also the false starts and higher-order thinking skills that lead to the solutions of problems.
- A consultant who helps individuals, small groups, or the whole class to decide if their work is keeping 'on track' and making reasonable progress.
- A moderator who poses questions to consider but leaves much of the decision making to the class.
- An interlocutor who supports students during class presentations, encouraging them to reflect on their activities and to explore mathematics on their own.
- A questioner who challenges students to make sure that what they are doing is reasonable and purposeful and who ensures that students can defend their conclusions."
(Counting on You, 1991, pp. 13-14)
Organizing the Content
|
Identifying the Problem The Mathematics Curriculum Committee for the Busytown School District began their discussions by reviewing how the present curriculum seemed to be working.
As they worked, the teachers discovered that their curriculum tended to break mathematics content down into very small, isolated bits of content that were often taught in isolation. Students just were not putting those bits together to form broader understandings of concepts. |
The approach taken by the teachers in this district is not unfamiliar. For many years, the mathematics curriculum has been viewed as a fragmented collection of discrete, isolated topics. Each topic has typically been broken down into its component tasks, with lessons focussing on each of these tasks. Students often fail to see the connections among the component tasks, working instead with each task in isolation.
Students often learn topics through rote manipulation of symbols rather than developing an understanding of a concept for themselves; this leads to rapid "forgetting" and a need for continual reteaching of concepts. The "spiral curriculum" (see Bruner, 1977) seems to have degenerated into "going around in circles," teaching and reteaching the same content year after year after year.
What Bruner's spiral curriculum actually suggests is that there is a set of simple but powerful basic ideas in mathematics (like functions and variables) that are central to the curriculum and that can begin to be addressed by students even at very young ages. These ideas are first addressed concretely in very basic forms. As students grow older, they revisit these ideas in more depth and learn to apply them in more complex and abstract situations. The ultimate goal is to develop a complete understanding of the basic ideas. Perhaps it is more useful to describe such a curriculum as a concentric one (see McKnight, et al., 1987) in which each encounter with an idea significantly moves learning to a deeper level.
The concentric/spiral approach originally suggested by Bruner can assist teachers and administrators in organizing the curriculum. The descriptions in this document of the content that New Jersey's students are expected to learn illustrates how students at each grade level can study the same topics in greater andgreater depth. In reading through the illustrations at each grade level, it is clear how understanding is expected to develop over the years.
Studying each of the content and process strands in isolation, however, is neither efficient nor effective. Students need to recognize related ideas within mathematics as well as those in other subject areas. They need to understand and appreciate the history of mathematics. They need to see that people are always developing new mathematics and new ways of learning mathematics. Students should learn mathematics through exploration, discovery, and problem solving. Thus, it is desirable to strive for integration of content across strands.
Units of Instruction
Most teachers think of mathematical content as being organized into instructional units. Frequently, these units correspond to the chapters in a textbook. They may also be organized in terms of mathematical or interdisciplinary themes. A unit usually includes investigations, problems, and other learning activities, integrated with assessment, that develop students' understanding of specific concepts. Units can be as short as a week or as long as six weeks, depending on the concepts and tasks involved. In units, it is important to include mathematics that makes sense all by itself, with a clear purpose. All the work in a unit should be related to a primary goal, exploring and eventually consolidating a set of related ideas that will be useful later. Furthermore, a unit should be interesting and engaging to the students, connecting to what they've learned before and helping them see mathematics as an integrated whole.
In planning for an instructional unit, teachers should first consider what concepts are central to the mathematics program at their particular grade level. The mathematical ideas in the unit should all fit together in a cohesive way, connecting to each other and to other areas of mathematics. Some important connections to consider in planning include what students have already learned and what students will be learning in the future, either in that grade or in future grades. Teachers may also want to consider what connections can be made to other subject areas. Activities included in the unit should focus on worthwhile mathematical tasks. The First Four Standards should be included in all instructional units, but not all units will deal with all content strands. Over the course of the year, however, students should have experiences with all of the content strands. Finally, teachers should consider what instructional and assessment strategies and activities are most likely to help them accomplish the goals they have established for that particular unit. By considering all of these components, teachers can design effective instructional units that will help to meet New Jersey's Mathematics Standards.
|
Components of an Instructional Unit
|
Not all mathematics need be done in units. It is also appropriate to include briefer activities unrelated to units. Such activities may be favorites from previous years, problems of the week, short exercises, and so on. Students also benefit from looking back across several units to identify related ideas.
The Appendix to this chapter contains three examples of instructional units. The first example describes the mathematics portions of an interdisciplinary unit in a primary classroom; this unit uses playgrounds as a theme for studying geometry and machines. The second example describes a teacher's thinking as he develops an introductory unit on common fractions for students in the middle grades. The third example shows high-school students using data analysis to generate mathematical models and to describe them with algebraic equations.
Daily Decisions
|
Ms. Kee was beginning a new school year in a new school district. She had talked with the mathematics supervisor and principal about the mathematics program in the school and had picked up copies of the textbook adopted for each course she would be teaching, as well as the district curriculum. She also had copies of materials she had used in her previous school, some of which she would like to continue using. She began working on eighth grade math by looking through the textbook and reading over the district curriculum. One of the first things she noticed was that the district curriculum specified thematic units to be taught over the course of the year, with references to specific pages in the text as well as some other materials. "This district curriculum is a big help! I'm glad I won't be just following the text this year. I need to talk to Mrs. Hughes again, though, to find out about all these other resources." "Let's see -- what else do I need to figure out? I want to look at different ways to handle homework and review. I've also been reading a lot about alternative assessment; I'd like to try some different techniques this year. And ..." |
Organizing the curriculum at the classroom level requires different kinds of decisions - decisions such as those Ms. Kee is facing: homework, review, assessment, lessons and emphasis.
While teachers must teach mathematics every day and must plan for a daily mathematics lesson, it is not necessary to teach a different objective each day. Such an approach reinforces a view of mathematics as isolated concepts. More desirable is a structure in which most lessons involve more than one objective addressed over several days in a more unified way. This approach provides the time that is needed for concepts to build, allowing daily lessons to be more connected Students may explore a concept one day, look for patterns the next, generalize their results on a third day, and apply those generalizations on a fourth day. Review is provided for in each lesson, building on previously-learned concepts and making explicit connections to other mathematical ideas.
Traditionally, students are given daily homework and/or classwork assignments from the textbook. These are to be done individually and often involve "drill and practice." A steady diet of such assignments is not desirable. The purpose of homework is not only to provide practice but also to help students identify what they do and do not understand by raising questions to be answered the next day in class. Thus it is desirable to have a variety of homework assignments, including exploration, projects, discovery, and writing in journals. Some assignments may extend over several days and may require considerable time outside of class. These assignments usually are stated in the form of a broad, complex problem to be investigated by a group of students, with findings presented in the form of an individual or group report, a presentation to the class, or some other type of visual display.
Testing has always been considered extremely important in the mathematics classroom. Traditionally, tests closely match assignments, with a narrow focus on skills. Mastery is expected. More desirable is use of a range of forms of assessment, including checking for understanding throughout a lesson, providing guided practice for students in class, quizzes, observation, interviews, and group work. Tests shouldinclude questions that ask students to explain their thinking. Students may be expected to keep portfolios of work throughout the year, revising their work to meet the expected standards.
In the vignette below, Mr. Fry begins to make some decisions about pacing, assignments, and review.
|
Mr. Fry has been teaching at New Jersey High School for the past fifteen years. He is very familiar with the district curriculum and with the textbooks but has become increasingly unhappy with his students' performance in geometry over the past few years. Last spring he was able to attend a mathematics conference and got some new ideas for ways to organize his geometry course. He also got some good ideas about using writing in the mathematics classroom and about integrating review activities into instruction on a regular basis. Now he is planning for next week's lessons on angle relationships. First, Mr. Fry looks over the text and reviews what he did last year. "Not too much student involvement - I need to get them thinking about what will happen before I state the theorems. Maybe I can find or develop some investigations that will get them started on vertical angles and linear pairs and ..." Mr. Fry develops some brief activities that will help the students discover the general relationships for themselves. "Now, I'd better think about how much time I want to spend on angle relationships. These are pretty important, so I don't want to rush through. On the other hand, the students will see these ideas again and again throughout the course. I think one week ought to be about right." Mr. Fry balances the competing needs of all the topics in the course with the need to develop understanding on the part of the students. Mr. Fry looks at the assignments he gave last year. "These were all pretty computational. I'll use some of these, but I think I'll take out some and have students write something each night. Then we can begin reviewing the homework by having them exchange what they wrote and comment on it." "What about review? I could add a few review problems to each homework assignment ... that would work well on Monday and Wednesday. On Tuesday and Thursday, I could begin class with a few review questions. And Friday, we'll do this project; it involves all of the ideas from this week plus some others they've already studied." Mr. Fry selects different strategies for incorporating review into each day's lesson. As for assessment, Mr. Fry uses a system that includes homework, classwork, tests, quizzes, journals, and group work. "This week, I'll give a homework quiz on Wednesday, and I'll grade their journals on Friday. I think I'll focus on how well the groups monitor their progress in working on Friday's project, too. The students should be ready for a written test next Friday." |
 |
SUGGESTIONS |
 Plan most lessons so that they involve more than one objective
and take place over more than one day, giving students enough time to
explore a situation thoroughly and solidify learning.
Plan most lessons so that they involve more than one objective
and take place over more than one day, giving students enough time to
explore a situation thoroughly and solidify learning.
 Provide for ongoing review in each lesson.
Provide for ongoing review in each lesson.
 Vary the types of homework assignments given to students,
including some projects and group assignments.
Vary the types of homework assignments given to students,
including some projects and group assignments.
 Use several different types of assessments and include
"explain" questions on written tests.
Use several different types of assessments and include
"explain" questions on written tests.
References
-
Artzt, Alice, and Claire Newman. How to Use Cooperative Learning in the Mathematics
Class.Reston, VA: NCTM, 1990.
Brooks, J. G., and M. G. Brooks. In Search of Understanding: The Case for Constructivist Classrooms. Alexandria, VA: Association for Supervision and Curriculum Development, 1993.
Bruner, J. S. The Process of Education. Cambridge, MA: Harvard University Press, 1977.
Burns, M. A Collection of Math Lessons. New Rochelle, NY: The Math Solution Publications, 1987.
Hart, L. and J. Walker. "The Role of Affect in Teaching and Learning Mathematics," in D. Owens, Ed. Research Ideas for the Classroom: Middle Grades Mathematics. New York: Macmillan, 1993.
Chazan, Daniel, and Richard Houde. How to Use Conjecturing and Microcomputers to Teach
Geometry. Reston, VA: National Council of Teachers of Mathematics, 1989.
Davidson, Neil, Ed. Cooperative Learning in Mathematics: A Handbook for Teachers. Menlo
Park, CA: Addison-Wesley, 1990.
DeBellis, V. A. Interactions between affect and cognition during mathematical problem solving: A two year case study of four elementary school children. (Doctoral Dissertation, Rutgers Univ.) Ann Arbor, MI: Univ. Microfilm 96-30716.
Johnson, David. Every Minute Counts: Making Your Math Class Work. Palo Alto, CA: Dale Seymour Publications, 1982.
Kamii, C. K. Young Children Reinvent Arithmetic. New York, NY: Teachers College Press, 1985.
Mathematical Sciences Education Board, National Research Council. Counting on You: Actions Supporting Mathematics Teaching Standards. Washington, DC: National Academy Press, 1991.
McKnight, C. C., et al. The Underachieving Curriculum: Assessing U. S. School Mathematics from an International Perspective. Champaign, IL: Stipes, 1987.
McLeod, D. B. "The Role of Affect," in E. Fennema, T. Carpenter, & S. Lamon, Eds. Integrating Research on Teaching and Learning Mathematics. Albany, NY: SUNY Press, 1991.
McLeod, D. B. and M.Ortega. "Affective Issues in Mathematics Education," in P. S. Wilson, Ed. Research Ideas for the Classroom: High School Mathematics. New York: Macmillan, 1993.
Meyer, M. R. "The Prediction of Mathematics Achievement and Participation for Females and Males: A Longitudinal Study of Affective Variables." Doctoral dissertation, University of Wisconsin-Madison. Dissertation Abstracts International, 47, 819A, 1986.
National Council of Teachers of Mathematics. Professional Standards for Teaching Mathematics. Reston, VA: NCTM, 1991.
National Research Council. Everybody Counts: A Report to the Nation on the Future of Mathematics Education. Washington, DC: National Academy Press, 1989.
Prichard, M. S., and S. Bingaman. "Instructional Activities and Decisions" in P. Wilson, Ed. Research Ideas for the Classroom: High School Mathematics. New York: Macmillan, 1993.
Renga, S. and L. Dalla. "Affect: A Critical Component of Mathematical Learning in Early Childhood," in R. Jensen, Ed. Research Ideas for the Classroom: Early Childhood Mathematics. New York: Macmillan, 1993.
Slavin, R. "Student Team Learning in Mathematics," in N. Davidson, Ed. Cooperative Learning in Math: A Handbook for Teachers. Reading, MA: Addison-Wesley, 1990.
Tobin, K. HM Study Skills. Newton, MA: HM Study Skills Group/NASSP/NAESP.
Appendix
A. Primary Grades Sample Unit - Geometry
This second-grade unit focuses on the playground as a context for studying geometric figures and properties as well as simple machines. In addition to the connections between mathematics and science, the teacher wanted to try to incorporate some language arts activities into the unit. She began her planning by reviewing New Jersey's Mathematics Standards and identifying the important mathematical concepts that would be addressed in the unit. She adapted a number of the cumulative progress indicators, primarily relating to Standard 7 (Geometry and Spatial Sense), and developed the following list of expectations for this unit.
- Students will explore and understand properties of three-dimensional and two-dimensional geometric shapes.
- Students will identify and use geometric shapes in various orientations: circle, square, rectangle, triangle, sphere, cone, cylinder, prism, pyramid.
- Students will explore properties of geometric shapes in conjuction with the concepts of area and perimeter.
- Students will develop tessellations.
- Students will explore the various ways geometric shapes and objects can be measured.
- Students will identify examples of congruent objects, similar objects, and self-similar objects.
- Students will identify the types of symmetry found on the playground, including both line symmetry and rotational symmetry.
- Students will use shadows (projections), points-of-view (perspective), and maps to describe the relationships among objects on the playground.
She next considered what connections students should make to other areas of mathematics; she decided that she would like to try to incorporate some measurement and some data collection and analysis. She also thought about how this unit could build on what students already knew. The second-graders had studied a little bit of geometry last year and they had worked with geometric figures in creating and extending patterns, but she knew that there was a wide range of understanding about some of the specific properties of different shapes. She decided to use several activities that would have students describe what they already knew as a springboard for further discussion. She thought about the unit later in the year that would develop linear measurement, perimeter, and area more formally; she decided to include measurement of shadows and an activity with designing a tile patio to begin to develop some of these ideas more informally. She also thought that, by having students build models of playground equipment, some size issues might arise naturally. Then the teacher considered the First Four Standards. She decided that she wanted to incorporate all four into the unit, but that she would emphasize connections and communication.
Next the teacher considered whether her initial ideas for activities represented worthwhile mathematical tasks. She thought that collecting examples of shapes, building playground models, planning a tile patio, and collecting data about shadows would be interesting to the students, that the activities would draw onstudents' previous experiences, and that the activities would stimulate connections within mathematics and across subject areas. She planned to build sufficient time into the unit for students to reflect on and discuss each of the activities. She also considered whether the instructional strategies she planned to use were appropriate and addressed different learning styles. She planned to include some work in cooperative groups, some work in pairs, and some individual work. She planned to have some oral work and some written work. She planned for projects, work with concrete materials, discovery learning, and whole-class discussions. She thought these would be sufficiently varied for her students.
Finally, the teacher thought about assessment. She knew she had already built into the instructional activities a number of assessment tasks, ranging from diagnostic activities, like writing about what they already know about triangles, to a summary assessment project, in which individual students would collect examples of different three-dimensional shapes. She wanted to be sure to provide for multiple measures of students' achievement. Student work in groups and comments in student journals would provide evaluative information on a daily basis. In addition to the independent project, she planned to randomly select students to report on group projects and, at the end of the unit, to give a quiz and ask students to evaluate their own learning in their journals.
Day 1: Shapes on the Playground. In math, the class goes on a geometry walk on the playground in order to check the list from science class and to find out what students already know about geometric shapes, congruence, similarity, self-similarity, and symmetry. Students look for examples of geometric ideas in nature and in objects found on the playground. Students take notes in their journals. Back in the classroom, during language arts, students write about and draw the geometric shapes they saw on the geometry walk. In science class, students make a list of types of equipment found on the playground. They discuss how the different objects found on the playground are alike and different. They generate a list of questions to investigate.
Day 2: Polygon Models. In math class, pairs of students use straws (cut to different lengths) and string to build models of figures composed of line segments (triangles, squares, rectangles, and possible others). Students discuss how all of the triangles (squares, rectangles, etc.) are alike and how they are different. The terms congruent, symmetric, similar, and self-similar are used. In science class, students study about the seesaw (lever), building models (what measurements do we need and why?), and investigating what happens when weights are placed at different locations on the lever.
Day 3: Polygon Properties. In math class, students continue their discussion of polygons. Groups of three or four students work together to write down what they know about triangles, squares, and rectangles and to list examples of these shapes found on the playground. They identify congruent and similar figures, as well as examples of self-similar shapes. They also describe lines of symmetry. They summarize what they have learned in their journals. In science class, students begin learning how each six of the simple machines - lever, inclined plane, wedge, pulley, wheel and axle, and gear wheel - work; they do tasks at learning stations set up for each machine.
Day 4: Investigating Shadows. In math class, students look at the shadows cast by simple objects placed on the overhead projector and make predictions about the shapes of the shadows cast by objects on the playground. They also discuss how the shapes of the shadows change as the sun moves through the sky and make predictions about how the shapes will change. They develop a plan for collecting data about the shadows made by the seesaw, the slide, the merry-go-round, and the swings throughout the next day. Agroup of students will be assigned to each object and will sketch the shape of the shadow and measure its length in links at three points during the day: 9 a.m., 11:30 a.m., and 2:00 p.m. In science class, students finish the learning station activity about simple machines.
Day 5: Collecting Shadow Data. At three points during the day, students go outside to sketch the shape of the shadows cast by each of the playground objects and to measure their size. On these outdoor excursions, they also look for examples of simple machines. At the end of the day, they list the different simple machines that they found, summarize the shadow data, identifying patterns in how the shadows changed, and write about how well their predictions from the previous day matched the actual data collected.
Day 6: Three-Dimensional Objects. The teacher begins the math lesson by showing the students the possible shadows of some mystery objects (ball, ice cream cone, soda can, a Unifix cube, and a pyramid from the kindergarten block corner) and asking the students to identify the objects. The students then discuss the mathematical terms for these three-dimensional objects and list objects on the playground (and elsewhere) that have those shapes. The teacher assigns a homework project to assess students' understanding and ability to identify shapes; the students must find five pictures in magazines of each of the shapes studied and write about why they chose those particular pictures. The project is due in one week. In science class, the students begin an investigation of swings (pendulums), looking at what factors affect how high the swing goes.
Day 7: Playground Models. Today the students begin working on building a model of an "ideal" playground. Since this is a primary class, the teacher has decided not to address the issue of scale directly, but rather to encourage students to compare the size of their models to those of other groups to see if they "match." Each group is assigned a piece of playground equipment to build. They are encouraged to build a model that "works" but are not required to do so. Students write in their journals about what they are doing in their groups.
Day 8: Finishing Models. The students finish their models and place them on a large board, creating their own class playground model. Each group explains their model. In language arts, they read a story that takes place on a playground.
Day 9: Playground Maps. Working in groups, the students sketch maps of their class playground model. In language arts, they begin writing their own playground stories.
Day 10: Orientation. Students place teddy bear counters on the playground maps according to clues given by task cards. They also sketch the orientation of the pieces of playground equipment that a specific teddy bear would see and check out their answers by using the actual model.
Day 11: Transformations. The students investigate transformations by making predictions about the positions of a teddy bear counter at various points on the slide, on the swing, and on the merry-go-round. They use their model to test their predictions. They also discuss the relationship between two teddy bears on the seesaw or opposite each other on the merry-go-round. The teacher then introduces the terms slide, flip, and turn, relating them to the students' findings. Students make sketches of each transformation in their journals.
Day 12: Tile Designs. Students investigate tessellations by designing a tile patio for a playground. Working in groups, they use pattern blocks to design a tessellation. They are given some constraints: (1) the distance around the patio must be at least 20 units, where the length of one side of the triangle is one unit; (2) the patio must be smaller than 40 squares; and (3) no more than $100 may be spent (costs for each shape are given).
Day 13: Tile Design Reports. Each group of students reports on their tile designs. In order to assess each students' contribution to the project, the teacher randomly selects a student from the group to answer some standard questions: How did you find the distance around your patio? Is it smaller than 40 squares? How do you know? How did you determine the cost of the patio?
Day 14: Quiz & Self-Assessment. Students take a short paper-and-pencil quiz and describe in their journals what they learned about geometry in this unit.
B. Middle Grades Unit - Common Fractions
Mr. Lopez is planning an introductory unit on common fractions for his sixth-grade class. Since this is a critical concept for sixth-graders to understand, he decides to focus almost exclusively on mathematics and deal more with applications in later units. From conversations with the fifth-grade teachers, he knows that the students worked at some length on fractions the previous year, using circle models to investigate fractions concretely. This year, he wants to extend the intuitive investigations to strips and rectangles and begin to develop the algorithms for addition, subtraction, multiplication, and division. His class has already studied decimals to some extent in connection with place value and the algorithms for addition and subtraction of whole numbers and decimals. He plans to use fractions extensively in the next two units, involving measurement and data analysis, and decides to postpone making connections to other subjects until that time. He also plans to introduce students to fraction calculators in the first of those units.
Mr. Lopez begins his planning by reviewing New Jersey's Mathematics Standards, and indentifying the important mathematical concepts to be addressed in this unit. He adapts a number of the cumulative progress indicators related to Standard 6 (Number Sense) and Standard 8 (Numerical Operations) and he develops the following list of expectations for this unit:
- Students will extend their number sense by constructing meanings for rational numbers.
- Students will expand the sense of magnitudes of different number types to include rational numbers.
- Students will develop and use order relations for rational numbers.
- Students will investigate the relationships among fractions, decimals, and percents and use all of them appropriately.
- Students will extend their understanding and use of basic arithmetic operations to fractions.
- Students will develop, analyze, apply, and explain procedures for computation and estimation with fractions.
From the First Four Standards, Mr. Lopez adapts the following expectations:
- Students will use mathematical language and symbols to represent problem situations and explain what they have done.
- Students will link conceptual and procedural knowledge.
- Students will understand and use various representations of concepts, and connect them to one another.
- Students will analyze mathematical situations by recognizing and using patterns and relationships.
From Standard 17 (Keys to Success), he selects the following for emphasis:
- Students will make conjectures, pose their own problems, devise their own approaches to problem solving and use their results for informed decision-making.
- Students will spend the time and use the tools needed for mathematical exploration and discovery.
- Students will gain confidence through successful experiences in mathematics and thereby develop a positive disposition toward doing mathematics.
- Students will regularly self-assess to determine the effectiveness of their strategies, the correctness of their results, and to monitor their attitudes toward learning mathematics.
Mr. Lopez makes a list of these expectations to keep in mind as the students proceed through the activities of the unit. Mr. Lopez next begins to outline a sequence of activities for the students. He first works in content blocks rather than days:
Different ways of writing numbers
Using strips to represent fractions
Equivalent fractions
Comparing fractions
Adding and subtracting fractions
Exploring multiplying fractions
Exploring dividing fractions
After outlining the activities, he goes back and tries to determine how many days should be in each block and what the specific activities should be for each day. While he is doing this, he begins thinking about how students will be assessed. He decides that he would like to use both quizzes and a project of some type. He plans to give a short paper-and-pencil quiz each week, including at least one question which requires the students to explain their thinking. In addition, he decides to have each student develop a book, The Story of Fractions. Students will complete individual pages for the book throughout the unit and assemble them at the end into a book to share with others. Mr. Lopez makes notes about some ideas for pages in conjunction with the activities he has outlined. As he makes his notes, he tries to make sure that he uses worthwhile mathematical tasks and a variety of instructional strategies.
A. Different ways of writing numbers
Day 1:
- Warmup: Write as many "incredible equations" as you can that have an answer of 123.
- Discuss warmup: 123 = 100 + 20 + 3 = 120 + 3 = 110 + 13
etc.
- (relate this idea to addition/subtraction algorithms)
- also 123 = 6 x 20 + 3 (when would writing 123 this way be useful?)
- Use base ten blocks, with 1 flat = 1 whole. How could we
describe 5 rods?
- 5/10 = 1/2 = 50/100 = 50% = .5 = .50
- When would writing the number in each way be useful? Example: 5 out of 10 games were won, 1 out of 2 apples were damaged, 50 out of 100 pennies or 50 cents, a 50% off sale, 5 dimes as a decimal is .5 as parts of a dollar, which is $.50, and so on.
- Have students work in small groups on several similar problems, and come up with as many different ways to write each number as they can. Remember to provide calculators! Post their results on the bulletin board. For homework, ask them to find examples from newspapers and magazines of the various notations that they used.
Day 2:
- Warmup: What are some different ways of writing 6/10? Discuss.
- Discuss the examples from newspapers and magazines that students found and have them put them on the bulletin board.
- Have students do more examples, using hundred grids instead of base ten blocks. This time, have students work individually and then compare their results in pairs before discussing them as a class.
- Make the point that we would like to be able to use whatever form of a number is easiest for computation.
- Remind students about work done with decimals and their connection to our curent focus on fractions. Homework assignment will be a decimal review.
- Note: Remember to come back to the idea of different ways of writing numbers again and again.
B. Using strips to represent fractions
Day 3:
- Warmup: Mental math with whole numbers and decimals.
- Have students use construction paper to make sets of
fraction strips by folding and cutting.
Students also keep one fraction worksheet without cutting it to refer to it later. Use different colors for each denominator. Make one set in class and have students make two more for homework. (Write up a handout with instructions.) - Ask the students questions about the strips, such as how many sixths make a whole? or which is bigger, a half or a third? Ask how we would write two thirds, developing the terms numerator and denominator.
- Use the strips to do problems, such as Suzanne ate a fourth of a candy bar and Luis ate a fifth of the candy bar. Who ate more candy? Be sure to point out the importance of making sure the candy bars were the same size, since a fourth of a small candy bar may be smaller than a fifth of a larger one. Bring in examples of candy bars to illustrate this concept. Also do some problems like Carmen ate half of a pizza and her sister ate one-fourth. How much was left? (This will begin to lay a foundation for later work with operations.)
- Have students create their first page for their fraction book by picking a number from a hat to give them the denominator for their fraction and completing a page entitled How Many Make a Whole?
- For homework, ask students to explain why 1/4 is bigger than 1/5.
C. Equivalent fractions
Day 4:
- Warmup: Mental math with decimals and whole numbers.
- Have students share what they wrote for homework with another student.
- Discuss homework as a group.
- Explain that today we will be working on different ways of naming the same fraction, or equivalent fractions. Relate this to a pizza that may be cut into halves or fourths or twelfths. Have students work in pairs to find different equivalent fractions for 1/2, 2/3, etc., using their fraction strips. Record their results on newsprint sheets. Introduce the idea of simplest form (using as few pieces as possible.)
- Use pattern blocks and one of the hexagons. Try to cover the hexagon with blocks of a new shape which uses the fewest pieces (2 trapezoids). Each represents 1/2 of the whole hexagon. Now cover it with the most pieces (6 triangles). Each is 1/6 of the hexagon. How many triangles cover one trapezoid? (3/6 = 1/2) Students use other pattern blocks to form equivalent names for fractions.
- Give students a challenge problem that cannot be done with their strips: Find as many equivalent fractions for 75/100 as you can. Are there other ways to write this number?
- Discuss the patterns that have emerged in looking at equivalent fractions: How can you tell if two fractions are equivalent?
- For homework, ask students to write about equivalent fractions: what are they, what have you learned, and what don't you understand?
Day 5:
- Warmup: Find simplest form for 2/4, 6/8, 8/10. Discuss.
- Have students work in groups of three on equivalent fraction problems, some where they fill in the missing numerator or denominator and some where they must put the fraction in simplest form. Include problems that can be done with the strips as well as some that cannot. While they are working, read over their homework and note the extent to which students are using the strips.
- Discuss the problems, having students explain how they solved each problem. (If students have alot of difficulty with these problems, divide into two days and repeat the activity.)
- Have students apply the methods discussed to several new problems as guided practice.
- Homework will be doing problems similar to those in class.
Day 6:
- Discuss homework. Quiz.
- Have students do another page for their book on What Are Equivalent Fractions?
D. Comparing fractions
Day 7:
- Warmup: Equivalent fractions.
- Return quizzes and discuss as needed.
- Use concrete real-life situation to pose question, How can we tell which of two fractions is larger?
- Write responses from class discussion on the board, then have students work in pairs, using concrete materials as needed, to compare pairs of fractions. Discuss.
- Homework will be similar to classwork.
Day 8:
- Warmup: Comparing fractions.
- Discuss homework. Compare some of the fractions found in newspapers and magazines that are posted on the bulletin board. Ask students when you might have to compare fractions in real life.
- Have students make up a word problem that requires comparing fractions.
- Have students complete another page for their fraction book on Which is bigger?
- Homework will be preparation for addition and subtraction of fractions: How can we express 1/4 + 1/4 as a single fraction? involving fractions with like denominators, followed by some word problems that require adding and subtracting fractions with like denominators.
E. Adding and subtracting fractions
Day 9:
- Warmup: Estimation with fractions - e.g., Which is closer to 1, 5/6 or 7/8?
- Discuss homework. Generalize procedure used to add and subtract fractions with like denominators.
- Pose problems involving fractions with unlike denominators: Mary ate 1/3 of a candy bar and Susie ate 1/6. How much did they eat all together? How can we express 1/3 + 1/6 as a single fraction?
- Have students explore this question in pairs, using their strips, then discuss what they did. Record what students did, using symbols.
- Have students do more problems involving unlike denominators (some word problems), using their strips and recording their results symbolically.
- Have students also do a subtraction problem with their strips: There was half of a candy bar left. Joe ate 1/3 of the candy bar. What fraction of the candy bar was left? Discuss results and record symbolically. How is this like the addition problems?
- For homework, have students do a few problems, including word problems and one that cannot be done with strips.
- Note: This may be too much for one day.
Day 10:
- Warmup: Estimation with fraction addition and subtraction. Discuss.
- Discuss homework. Lead students to idea that you need to express fractions as equivalent fractions which have a common denominator.
- Have students do a few addition and subtraction problems (some that can be checked with strips and some not, some word problems and some not) and discuss.
- Homework: Problems involving addition and subtraction of unlike and like fractions, including word problems.
Day 11:
- Warmup: Estimation with fraction addition and subtraction. Discuss.
- Discuss homework. Quiz. Have students do two more pages for their fraction books on How to Add Fractions and How to Subtract Fractions. Have them make up one word problem to include on each page.
- Homework: Finish fraction book pages.
F. Exploring multiplying fractions
Day 12:
- Warmup: Mental math with fraction addition and subtraction. Discuss.
- Introduce each of the following expressions with a word
problem, discuss what the expression
means and ask students how to represent them concretely:
-
3 x 1/4 (3 groups of 1/4, or 3/4) 1/3 x 12 (1/3 of a group of 12, or 4) 1/2 x 1/3 (1/2 of 1/3, or 1/6 - fold a 1/3 strip in half vertically or horizontally)
-
- Have students work in groups to do similar problems concretely, recording their results symbolically and looking for patterns.
- Homework: Explain what each problem means and solve it: 2 x 1/6, 2/3 x 9, 2/3 x 1/2.
Day 13:
- Warmup: Equivalent fractions, comparing fractions
- Discuss homework. Have different students explain different ways they solved the problems.
- For class, have students do more multiplication problems and then do another page for their fraction book on Multiplying Fractions. Have them include at least one word problem on each page.
G. Exploring dividing fractions
Day 14:
- Warmup: Estimation with fraction multiplication
- Discuss homework.
- Focus on developing meaning for division by asking students
to solve some word problems
involving the following expressions:
-
6 ÷ 2 How many groups of 2 are there in 6? or What do you get when you divide 6 into 2 equal parts? Is this like another problem we have done recently (1/2 x 6?) 1/2 ÷ 3 What do you get when you divide one-half into three equal parts? Ask if this reminds them of another problem they have done recently, like 1/3 x 1/2. 6 ÷ 1/2 How many halves are there in 6? 1/2 ÷ 1/6 How many sixths are there in a half?
-
- Give pairs of students a set of problems to explain the meaning of, represent concretely, and solve.
- Ask them to look for patterns.
- For homework, ask students to write about what they have found out about dividing with fractions.
Day 15:
- Warmup: Mental math with fractions
- Have students trade homework papers and comment: Do they agree? Is it clear?
- Have students do more division problems, including word problems and one or two that cannot be done with strips. Discuss their procedures.
- Homework: Division of fractions problems, including word problems.
Day 16:
- Warmup: Estimation with fractions.
- Discuss homework. Quiz.
- Have students complete the last page of their fraction book on Dividing Fractions and the cover.
- Homework: finish fraction book.
H. Unit summary
Day 17:
- Review of unit, including binding Fraction Book.
Day 18:
- Review of unit - make up some kind of game?
Day 19:
- Unit test - be sure to include some questions which ask students to explain their thinking.
C. High School Sample Unit - What's My Line?
Ms. Albert's students have been working with solving equations and graphing lines, including learning about slopes and intercepts. They just finished a statistics unit in which they learned how to make stem-and-leaf plots and boxplots. In both these units, they have been using graphing calculators to graph equations and to generate one-variable statistical information and graphs. Now Ms. Albert would like to have them work with some real data involving applications of linear equations. She has been talking with the science teacher about some possible links between mathematics and science. She thinks that this work will provide an important foundation as they begin to look at systems of equations and quadratics. She hopes to include another unit like this one, using a greater variety of types of equations, later in the year.
She begins her planning by reviewing New Jersey's Mathematics Standards. She is somewhat surprised to find that while the unit focuses primarily on Standard 13 (Algebra) and Standard 12 (Probability and Statistics), it can also easily include some elements of Standard 15 (Building Blocks of Calculus). She also decides that the unit should include work on Standard 1 (Problem Solving), Standard 2 (Communicating Mathematics), and Standard 5 (Tools and Technology). She adapted a number of cumulative progress indicators and developed the following list of expectations for this unit.
- Students will model and solve problems that involve varying quantities with variables, expressions, and equations.
- Students will interpret algebraic equations geometrically and describe geometric objects algebraically.
- Students will represent, analyze, and predict changes of quantities over time using linear and non-linear models.
- Students will use linear and non-linear models to explain growth and change in the natural world, such as situations involving motion, periodic phenomena, and biological and economic growth.
- Students will use curve fitting to interpolate and predict from data.
- Students will construct and use graphical and symbolic models to represent problem situations.
- Students will determine, collect, organize, and analyze data needed to solve problems.
- Students will effectively apply processes of mathematical modeling in mathematics and other areas.
- Students will use mathematical language and symbols to represent problem situations and explain what they have done.
- Students will explain their conclusions, thought processes, and strategies in problem-solving situations.
- Students will use technology to gather, analyze, and display mathematical data.
Ms. Albert continues her planning by preparing an outline of the unit. As she works, she keeps in mind the components of an effective instructional unit, especially using a variety of instructional strategies and making sure that tasks are worthwhile mathematically. She also considers assessment as she plans, incorporating a paper-and-pencil test at the end of the unit, written projects done in pairs, and homeworkassignments done individually most nights.
Day 1: Posing a Problem. The class begins with a problem: Archaeologists have found a human thigh bone that is 38 cm long in a dig in New Jersey. They would like to use this bone to estimate the height of the person from which it came. How might they do this? After some discussion, the class decides to collect data on the length of their thigh bones (as accurately as they can measure them) and their height. For homework, they each collect data from five other individuals of varying ages.
Day 2: Finding a Line Freehand. The students enter their data individually into their own graphing calculators at a prescribed location. The teacher then connects all of the calculators to assemble a complete data set. (If this cannot be done, then the class data is collected and entered into the calculator for the overhead projector.) The class decides to look at a scatterplot of the data. They decide that the data seem to fall more or less in a straight line. Using trial and error and working in pairs, the students suggest some potential equations for lines to use to describe the relationship between the length of the thigh bone (x) and the height of a person (y). For homework, each student uses a given set of data to make a scatterplot and determine a line that fits by using trial and error.
Day 3: Median-Median Line. After discussing the homework, the students learn how to find a median-median line, using their thigh bone vs. height data set. They compare the equation generated in this way with the equations they generated freehand. The teacher introduces the concept of residuals, the vertical distances between the line of best fit and each point in the data set. The students discuss the advantages and disadvantages of the freehand method and the median-median line method. For homework, they use the same data set as the previous night, finding the median-median line and the residuals for each point in the data set. (The median-median line, available on many calculators which have statistics capabilities, is found by dividing the data points on the x-y plane into three equal sets, grouped by x-value, finding a single point for each set whose coordinates are the medians of the respective coordinates of the points in the set, connecting the first and third points by a straight line, and shifting this line 1/3 of the way toward the second point. The median-median line is discussed in Contemporary Precalculus through Applications by the North Carolina School of Science and Mathematics, Janson Publications, 1991.)
Day 4: Regression Line. The teacher develops the idea of using the principle of least squares to find a line of best fit (regression line) and shows the class how to use their calculators to do this with their thigh bone vs. height data set. The class compares this equation to those generated using the freehand and median-median line methods. They discuss the advantages and disadvantages of each method. For homework, the students find the least squares regression line for the data set they have been using previously for homework.
Day 5: Unit Projects. Today the students begin working on their unit projects. Each pair of students has two problems to investigate. One problem requires them to collect data, either on the circumference and diameter of round objects, the length of a person's foot versus her/his height, the height of a candle as it burns, or a simulation of decay in which the students monitor the number of M&Ms that remain after each trial, involving spilling the M&Ms from a cup, when those that land M-side up are removed. The other problem provides a data set for the students: temperature and pressure data collected by chemistry students, cricket chirps per minute and temperature, the relationship between fouls committed in basketball and points scored, or the relationship between winning times in the Olympics for the 100-yard dash and the year. For each problem, the students must prepare a scatterplot and determine whether or not a linear relationship exists. If so, then they must use each of the three methods (freehand, median-median line, and linear regression) to find the equation of a line of best fit. They must then prepare a report explaining what they have done and why and discussing which line they feel best describes the data set and why.
Days 6-7: Unit Projects. Students continue working on their projects.
Day 8: Discussion and Review. Students hand in their completed projects and discuss their results. They also review for a test the following day.
Day 9: Test. The students take a paper-and-pencil test covering the concepts studied in this unit as well as the computational techniques used.
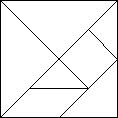 As the students folded the squares, Mr. Hudson continued to
question them. They told him that the shapes were two isosceles right
triangles, that the two triangles were congruent, and that each
triangle had one right angle and two 45 degree angles.
As the students folded the squares, Mr. Hudson continued to
question them. They told him that the shapes were two isosceles right
triangles, that the two triangles were congruent, and that each
triangle had one right angle and two 45 degree angles.