STANDARD 14 - DISCRETE MATHEMATICS
|
All students will apply the concepts and methods of discrete
mathematics to model and explore a variety of practical
situations.
|
Standard 14 - Discrete Mathematics - Grades 3-4
Overview
The five major themes of discrete mathematics, as discussed in the
K-12 Overview, are systematic listing, counting, and
reasoning; discrete mathematical modeling using graphs (networks) and
trees; iterative (that is, repetitive) patterns and processes;
organizing and processing information; and following and
devising lists of instructions, called
"algorithms," and using them to find the best
solution to real-world problems.
Despite their formidable titles, these five themes can be addressed
with activities at the 3-4 grade level which involve purposeful play
and simple analysis. Indeed, teachers will discover that many
activities that they already are using in their classrooms reflect
these themes. These five themes are discussed in the paragraphs
below.
The following discussion of activities at the 3-4 grade levels
in discrete mathematics presupposes that corresponding
activities have taken place at the K-2 grade levels. Hence 3-4 grade
teachers should review the K-2 grade level discussion of
discrete mathematics and use might use activities similar to those
described there before introducing the activities for this
grade level.
Activities involving systematic listing, counting, and
reasoning should be done very concretely at the 3-4 grade levels,
building on similar activities at the K-2 grade levels. For example,
the children could systematically list and count the total number of
possible combinations of dessert and beverage that can be selected
from pictures of those two types of foods they have cut out of
magazines or that can be selected from a restaurant menu. Similarly,
playing games like Nim, dots and boxes, and dominoes becomes a
mathematical activity when children systematically reflect on the
moves they make in the game and use those reflections to decide on the
next move.
An important discrete mathematical model is that of a
graph, which is used whenever a collection of things are joined
by connectors - such as buildings and roads, islands and bridges,
or houses and telephone cables - or, more abstractly, whenever
the objects have some defined relationship to each other; this kind of
model is described in the K-2 Overview. At the 3-4 grade levels,
children can recognize and use models of graphs in various ways, for
example, by finding a way to get from one island to another by
crossing exactly four bridges, or by finding a route for a city mail
carrier which uses each street once, or by constructing a
collaboration graph for the class which describes who has worked with
whom during the past week. A special kind of graph is called a
"tree." Three views of the same tree are pictured in the
diagram below; the first suggests a family tree, the second a tree
diagram, and the third a "real" tree.
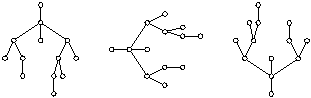
At the 3-4 grade levels, students can use a tree diagram to
organize the six ways that three people can bearranged in order. (See
the Grades 3-4 Indicators and Activities for an example.)
Students can recognize and work with repetitive patterns and
processes involving numbers and shapes, with classroom objects and
in the world around them. Children at the 3-4 grade levels are
fascinated with the Fibonacci sequence of numbers 1, 1, 2, 3, 5, 8,
13, 21, 34, 55, 89, ... where every number is the sum of the previous
two numbers. This sequence of numbers turns up in petals of flowers,
in the growth of populations (see the activity involving rabbits), in
pineapples and pine cones, and in lots of other places in nature.
Another important sequence to introduce at this age is the doubling
sequence 1, 2, 4, 8, 16, 32, ... and to discuss different situations
in which it appears.
Students at the 3-4 grade levels should investigate ways of
sorting items according to attributes like color or
shape, or by quantitative information like size, arranging data
using tree diagrams and building charts and tables, and recovering
hidden information in games and encoded messages. For example,
they can sort letters into zip code order or sort the class
alphabetically, create bar charts based on information obtained
experimentally (such as soda drink preferences of the class), and play
games like hangman to discover hidden messages.
Students at the 3-4 grade levels should describe and discuss
simple algorithmic procedures such as providing and following
directions from one location to another, and should in simple cases
determine and discuss what is the best solution to a problem.
For example, they might follow a recipe to make a cake or to assemble
a simple toy from its component parts. Or they might find the best
way of playing tic-tac-toe or the shortest route that can be used to
get from one location to another.
Two important resources on discrete mathematics for teachers at all
levels are the 1991 NCTM Yearbook Discrete Mathematics Across the
Curriculum K-12 and the 1997 DIMACS Volume Discrete Mathematics
in the Schools: Making An Impact. Another important
resource for 3-4 teachers is This Is MEGA-Mathematics!
Standard 14 - Discrete Mathematics - Grades 3-4
Indicators and Activities
The cumulative progress indicators for grade 4 appear below in
boldface type. Each indicator is followed by activities which
illustrate how it can be addressed in the classroom in grades 3 and
4.
Building upon knowledge and skills gained in the preceding grades,
experiences will be such that all students in grades 3-4:
1. Explore a variety of puzzles, games, and
counting problems.
- Students read One Hundred Hungry Ants by
Elinor Pinczes and then illustrate and write their own story books
(perhaps titled 18 Ailing Alligators or 24 Furry
Ferrets) in a style similar to the book using as many different
arrangements of the animals as possible in creating their books. They
read their books to students in the lower grades.
- Students count the number of squares of each
size (1x1, 2x2, 3x3, 4x4, 5x5) that they can find on a geoboard, and
in larger square or rectangular grids.
- Students determine the number of possible combinations of
dessert and beverage that could be selected from pictures of those two
types of foods they have cut out of magazines. Subsequently, they
determine the number of possible combinations of dessert and beverage
that could be chosen from a restaurant menu, and how many of those
combinations could be ordered if they only have $4.
- Students find the number of different ways to make a row of
four flowers each of which could be red or yellow. They can model
this with Unfix cubes and explain how they know that all combinations
have been obtained.
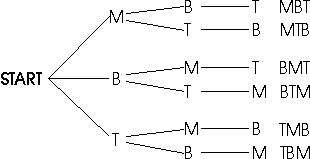
- Students determine the number of different ways any three
people can be arranged in order, and use a tree diagram to organize
the information. The tree diagram below represents the six ways that
Barbara (B), Maria (M), and Tarvanda (T), can be arranged in order.
The three branches emerging from the "start" position
represent the three people who could be first; each path from left to
right represents the arrangement of the three people listed to the
right.
- Each student uses four squares to make designs where each
square shares an entire side with at least one of the other three
squares. Geoboards, attribute blocks or Linker cubescan be used.
How many different shapes can be made? These shapes are called
"tetrominoes."
- Each group of students receives a bag containing four
colored beads. One group may be given 1 red, 1 black and 2 green
beads; other groups may have the same four beads or different ones.
Students take turns drawing a bead from the bag, recording its color,
and replacing it in the bag. After 20 beads are drawn, each group
makes a bar graph illustrating the number of beads drawn of each
color. They make another bar graph illustrating the number of beads
of each color actually in the bag, and compare the two bar graphs. As
a follow-up activity, students should draw 20 or more times from a bag
containing an unknown mixture of beads and try to guess, and justify,
how many beads of each color are in the container.
- Students determine what amounts of postage can and cannot
be made using only 3 cent and 5 cent stamps.
- Students generate additional rows of Pascal's
triangle (at right). They color all odd entries one color and all
even entries another color. They examine the patterns that result,
and try to explain what they see. They discuss whether their
conclusions apply to a larger version of Pascal's triangle.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
- Students make a table indicating which stamps of the
denominations 1 cent, 2 cents, 4 cents, 8 cents, 16 cents, 32 cents
would be used (with no repeats) to obtain each amount of postage from
1 cent to 63 cent. For the table, they list the available
denominations across the top and the postage amounts from 1 cent to
63 cents at the left; they put a checkmark in the appropriate spot if
they need the stamp for that amount, and leave it blank otherwise.
They try to find a pattern which could be used to decide which amounts
of postage could be made if additional stamps (like 64 cents and
128 cents) were used.
- Students play games like Nim and reflect on the moves they
make in the game. (See Math for Girls and Other Problem
Solvers, by D. Downie et al., for other games for this grade
level.) In Nim, you start with a number of piles of objects -
for example, you could start with two piles, one with five buttons,
the other with seven buttons. Two students alternate moves, and each
move consists of taking some or all of the buttons from a single pile;
the child who takes the last button off the table wins the game. Once
they master this game, students can try Nim with three piles, starting
with three piles which have respectively 1, 2, and 3 buttons.
- Students play games like dots and boxes
and systematically think about the moves they make in the game.
In dots and boxes, you start with a square (or rectangular) array of
dots, and two students alternate drawing a line which joins two
adjacent dots. Whenever all four sides of a square have been drawn,
the student puts her or his initial in the square and draws another
line; the person with initials in more squares wins the
game.
2. Use networks and tree diagrams to represent
everyday situations.
- Students make a collaboration graph for the members of the
class which describes who has worked with whom during the past
week.
- Students draw specified patterns on the chalkboard without
retracing, such as those below. Alternatively, they may trace these
patterns in a small box of sand, as done historically in African
cultures. (See Ethnomathematics, Drawing Pictures With One
Line, or Insides, Outsides, Loops, and Lines.)
Alternatively, on a pattern of islands and bridges laid out on the
floor with masking tape, students might try to take a walk which
involves crossing each bridge exactly once (leaving colored markers on
bridges already crossed); note that for some patterns this may not be
possible. The patterns given here can be used, but students can
develop their own patterns and try to take such a walk for each
pattern that they create.
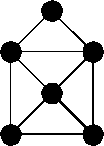
-
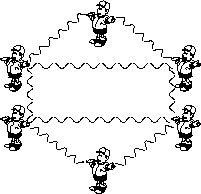 Students create "human graphs" where
they themselves are the vertices and they use pieces of yarn (several
feet long) as edges; each piece of yarn is held by two students, one
at each end. They might create graphs with specified properties; for
example, they might create a human graph with four vertices of degree
2, or, as in the figure at the right, with six vertices of which four
have degree 3 and two have degree 2. (The degree of a vertex is
the total number of edges that meet at the vertex.) They might count
the number of different shapes of human graphs they can form with four
students (or five, or six).
Students create "human graphs" where
they themselves are the vertices and they use pieces of yarn (several
feet long) as edges; each piece of yarn is held by two students, one
at each end. They might create graphs with specified properties; for
example, they might create a human graph with four vertices of degree
2, or, as in the figure at the right, with six vertices of which four
have degree 3 and two have degree 2. (The degree of a vertex is
the total number of edges that meet at the vertex.) They might count
the number of different shapes of human graphs they can form with four
students (or five, or six).
- Students use a floor plan of their school to map out
alternate routes from their classroom to the school's exits, and
discuss whether the fire drill route is in fact the shortest route to
an exit.
- Students draw graphs of their own neighborhoods, with
edges representing streets and vertices representing locations where
roads meet. Can you find a route for the mail carrier in
your neighborhood which enables her to walk down each street, without
repeating any streets, and which ends where it begins? Can you
find such a route if she needs to walk up and down each street
in order to deliver mail on both sides of the street?
- Students color maps (e.g., the 21 counties of New Jersey)
so that adjacent counties (or countries) have different colors, using
as few colors as possible. The class could then share a NJ cake
frosted accordingly. (See The Mathematician's Coloring
Book.)
- Students recognize and understand family trees in social
and historical studies, and instories that they read. Where
appropriate, they create their own family trees.
3. Identify and investigate sequences and patterns found
in nature, art, and music.
- Students read A Cloak for a Dreamer by
A. Friedman, and make outlines of cloaks or coats like those worn by
the sons of the tailor in the book by tracing their upper bodies on
large pieces of paper. Students could use pattern blocks or pre-cut
geometric shapes to cover (tessellate) the paper cloaks with patterns
like those in the book or try to make their own cloth
designs.
- Students read Sam and the Blue Ribbon
Quilt by Lisa Ernst, and by rotating, flipping, or sliding cut-out
squares, rectangles, triangles, etc., create their own symmetrical
designs on quilt squares similar to those found in the book. The
designs from all the members of the class are put together to make a
patchwork class quilt or to form the frame for a math bulletin
board.
- Students take a "pattern walk" through
the neighborhood, searching for patterns in the trees, the houses, the
buildings, the manhole covers (by the way, why are they always
round?), the cars, etc.; the purpose of this activity is to
create an awareness of the patterns around us. By
Nature's Design is a photographic journey with an eye
for many of these natural patterns.
-
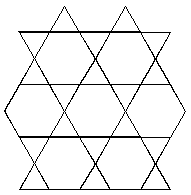 Students "tessellate" the plane using
squares, triangles, or hexagons to completely cover a sheet of paper
without overlapping. They also tessellate the plane using groups of
shapes, like hexagons and triangles as in the figure at the
right.
Students "tessellate" the plane using
squares, triangles, or hexagons to completely cover a sheet of paper
without overlapping. They also tessellate the plane using groups of
shapes, like hexagons and triangles as in the figure at the
right.
- Students might ask if their parents would be willing to
give them a penny for the first time they do a particular chore, two
pennies for the second time they do the chore, four pennies for the
third time, eight pennies for the fourth time, and so on. Before
asking, they should investigate, perhaps using towers of Unifix cubes
that keep doubling in height, how long their parents could actually
afford to pay them for doing the chore.
- Students cut a sheet of paper into two halves,
cut the resulting two pieces into halves, cut the resulting four
pieces into halves, etc. If they do this a number of times, say
12 times, and stacked all the pieces of paper on top of each
other, how high would the pile of paper be? Students
estimate the height before performing any calculations.
- Students color half a large square, then half of the
remaining portion with another color, then half of the remaining
portion with a third color, etc. Will the entire area ever get
colored? Why, or why not?
- Students count the number of rows of bracts on a
pineapple or pine cone, or rows of petals on an artichoke, or rows of
seeds on a sunflower, and verify that these numbers all appear in the
sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, ... of Fibonacci numbers, where
each number is the sum of the two previous numbers on the list.
Students find other pictures depicting Fibonacci numbers as they arise
in nature, referring, for example, to Fibonacci Numbersin
Nature. In Mathematical Mystery Tour by Mark Wahl, an
elementary school teacher provides a year's worth of Fibonacci
explorations and activities.
- Using a large equilateral triangle provided by
the teacher, students find and connect the approximate midpoints of
the three sides, and then color the triangle in the middle. (See
Stage 1 picture.) They then repeat this procedure with each of the
three uncolored triangles to get the Stage 2 picture, and then repeat
this procedure again with each of the nine uncolored triangles to get
the Stage 3 picture. These are the first three stages of the
Sierpinski triangle; subsequent stages become increasingly intricate.
How many uncolored triangles are there in the Stage 3
picture? How many would there be in the Stage 4 picture if the
procedure were repeated again?

4. Investigate ways to represent and classify
data according to attributes, such as shape or color, and
relationships, and discuss the purpose and usefulness of such
classification.
- Students are provided with a set of index cards on each of
which is written a word (or a number). Working in groups, students
put the cards in alphabetical (or numerical) order, explain the
methods they used to do this, and then compare the various methods
that were used.
- Students bring to class names of cities and
their zip codes where their relatives and friends live, paste these at
the appropriate locations on a map of the United States, and look for
patterns which might explain how zip codes are assigned. Then they
compare their conclusions with post office information to see whether
they are consistent with the way that zip codes actually are
assigned.
- Students send and decode messages in which each letter has
been replaced by the letter which follows it in the alphabet (or
occurs two letters later). Students explore other coding systems
described in Let's Investigate Codes and Sequences
by Marion Smoothey.
- Students collect information about the soft drinks they
prefer and discuss various ways of presenting the resulting
information, such as tables, bar graphs, and pie charts, displayed
both on paper and on a computer.
- Students play the game of Set in which
participants try to identify three cards from those on display which,
for each of four attributes (number, shape, color, and shading), all
share the attribute or are all different. Similar ideas can be
explored using Tabletop, Jr. software.
5. Follow, devise, and describe practical lists of
instructions.
- Students follow a recipe to make a cake or to assemble a
simple toy from its component parts, and then write their own versions
of those instructions.
- Students give written and oral directions for going from
the classroom to another room in the school, and represent these
directions with a diagram drawn approximately to scale.
- Students read Anno's Mysterious
Multiplying Jar by Mitsumasa Anno. During a second reading they
devise a method to record and keep track of the increasing number of
items in the book and predict how that number will continue to grow.
Each group explains its method to the class.
- Students write step-by-step directions for a simple task
like making a peanut butter and jelly sandwich, and follow them to
prove that they work.
- Students find and describe the shortest path from the
computer to the door or from one location in the school building to
another.
-
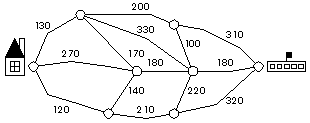 Students find the shortest route from school to home
on a map (see figure at right), where each edge has a specified
numerical length in meters; students modify lengths to obtain a
different shortest route.
Students find the shortest route from school to home
on a map (see figure at right), where each edge has a specified
numerical length in meters; students modify lengths to obtain a
different shortest route.
- Students write a program which will create specified
pictures or patterns, such as a house or a clown face or a symmetrical
design. Logo software is well-suited to this activity. In Turtle
Math, students use Logo commands to go on a treasure hunt, and
look for the shortest route to complete the search.
- Working in groups, students create and explain a fair way of
sharing a bagful of similar candies or cookies. (See also the
vignette entitled Sharing A Snack in the Introduction to this
Framework.) For example, if the bag has 30 brownies and there
are 20 children, then they might suggest that each child gets one
whole brownie and that the teacher divide each of the remaining
brownies in half. Or they might suggest that each pair of children
figure out how to share one brownie. What if there were 30 hard
candies instead of brownies? What if there were 25 brownies?
What if there were 15 brownies and 15 chocolate chip cookies?
The purpose of this activity is for students to brainstorm
possible solutions in the situations where there may be no solution
that everyone perceives as fair.
- Students devise a strategy for never losing at
tic-tac-toe.
-
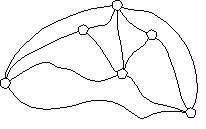 Students find different ways of paving just enough
streets of a "muddy city" (like the street map at the right,
perhaps laid out on the floor) so that a child can walk from any one
location to any other location along paved roadways. In "muddy
city" none of the roads are paved, so that whenever it rains all
streets turn to mud. The mayor has asked the class to propose
different ways of paving the roads so that a person can get from any
one location to any other location on paved roads, but so that the
fewest number of roads possible are paved.
Students find different ways of paving just enough
streets of a "muddy city" (like the street map at the right,
perhaps laid out on the floor) so that a child can walk from any one
location to any other location along paved roadways. In "muddy
city" none of the roads are paved, so that whenever it rains all
streets turn to mud. The mayor has asked the class to propose
different ways of paving the roads so that a person can get from any
one location to any other location on paved roads, but so that the
fewest number of roads possible are paved.
- Students divide a collection of Cuisenaire rods of
different lengths into two or three groups whose total lengths are
equal (or as close to equal as possible).
References
-
Anno, M. Anno's Mysterious Multiplying Jar.
Philomel Books, 1983.
Asher, M. Ethnomathematics. Brooks/Cole Publishing
Company, 1991.
Casey, Nancy, and Mike Fellows. This is MEGA-Mathematics!
- Stories and Activities for
Mathematical Thinking, Problem-Solving, and Communication.
Los Alamos, CA: Los Alamos National Laboratories, 1993. (A
version is available online at
http://www.c3.lanl.gov/mega-math)
Chavey, Darrah. Drawing Pictures with One Line: Exploring
Graph Theory. Consortium for Mathematics and Its Applications
(COMAP), Module #21, 1992.
Downie, D., T. Slesnick, and J. Stenmark. Math for Girls and
Other Problem Solvers. EQUALS. Lawrence Hall of
Science, 1981.
Ernst, L. Sam Johnson and the Blue Ribbon Quilt.
Mulberry Paperback Book, 1992.
Francis, R. The Mathematician's Coloring
Book. Consortium for Mathematics and Its Applications
(COMAP), Module #13, 1989.
Fibonacci Numbers in Nature. Dale Seymour
Publications
Friedman, A. A Cloak for a Dreamer. Penguin Books.
Scholastics.
Kenney, M. J., Ed. Discrete Mathematics Across the Curriculum
K-12. 1991 Yearbook of the National Council of Teachers of
Mathematics (NCTM). Reston, VA: 1991.
Kohl, Herbert. Insides, Outsides, Loops, and Lines. New
York: W. H. Freeman, 1995.
Murphy, P. By Nature's Design. San
Francisco, CA: Chronicle Books, 1993.
Pinczes, E. J. One Hundred Hungry Ants. Houghton Mifflin
Company, 1993.
Rosenstein, J. G., D. Franzblau, and F. Roberts, Eds.
Discrete Mathematics in the Schools:
Making an Impact. Proceedings of a 1992 DIMACS Conference
on "Discrete Mathematics in the Schools." DIMACS Series
on Discrete Mathematics and Theoretical Computer Science.
Providence, RI: American Mathematical Society (AMS), 1997.
(Available online from this chapter in
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/.)
Set. Set Enterprises.
Smoothey, Marion. Let's Investigate Codes and
Sequences. New York: Marshall Cavendish Corporation,
1995.
Tompert, Ann. Grandfather Tang's Story.
Crown Publishing, 1990.
Wahl, Mark. Mathematical Mystery Tour: Higher-Thinking Math
Tasks. Tucson, AZ: Zephyr Press, 1988.
Software
-
Logo. Many versions of Logo are commercially
available.
Tabletop, Jr. Broderbund Software. TERC.
Turtle Math. LCSI.
On-Line Resources
-
http://dimacs.rutgers.edu/archive/nj_math_coalition/framework.html/
The Framework will be available at this site during
Spring 1997. In time, we hope to post additional resources
relating to this standard, such as grade-specific activities submitted
by New Jersey teachers, and to provide a forum to discuss the
Mathematics Standards.
|


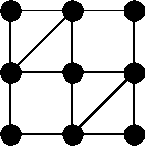
 Students create "human graphs" where
they themselves are the vertices and they use pieces of yarn (several
feet long) as edges; each piece of yarn is held by two students, one
at each end. They might create graphs with specified properties; for
example, they might create a human graph with four vertices of degree
2, or, as in the figure at the right, with six vertices of which four
have degree 3 and two have degree 2. (The degree of a vertex is
the total number of edges that meet at the vertex.) They might count
the number of different shapes of human graphs they can form with four
students (or five, or six).
Students create "human graphs" where
they themselves are the vertices and they use pieces of yarn (several
feet long) as edges; each piece of yarn is held by two students, one
at each end. They might create graphs with specified properties; for
example, they might create a human graph with four vertices of degree
2, or, as in the figure at the right, with six vertices of which four
have degree 3 and two have degree 2. (The degree of a vertex is
the total number of edges that meet at the vertex.) They might count
the number of different shapes of human graphs they can form with four
students (or five, or six). Students "tessellate" the plane using
squares, triangles, or hexagons to completely cover a sheet of paper
without overlapping. They also tessellate the plane using groups of
shapes, like hexagons and triangles as in the figure at the
right.
Students "tessellate" the plane using
squares, triangles, or hexagons to completely cover a sheet of paper
without overlapping. They also tessellate the plane using groups of
shapes, like hexagons and triangles as in the figure at the
right.
 Students find the shortest route from school to home
on a map (see figure at right), where each edge has a specified
numerical length in meters; students modify lengths to obtain a
different shortest route.
Students find the shortest route from school to home
on a map (see figure at right), where each edge has a specified
numerical length in meters; students modify lengths to obtain a
different shortest route. Students find different ways of paving just enough
streets of a "muddy city" (like the street map at the right,
perhaps laid out on the floor) so that a child can walk from any one
location to any other location along paved roadways. In "muddy
city" none of the roads are paved, so that whenever it rains all
streets turn to mud. The mayor has asked the class to propose
different ways of paving the roads so that a person can get from any
one location to any other location on paved roads, but so that the
fewest number of roads possible are paved.
Students find different ways of paving just enough
streets of a "muddy city" (like the street map at the right,
perhaps laid out on the floor) so that a child can walk from any one
location to any other location along paved roadways. In "muddy
city" none of the roads are paved, so that whenever it rains all
streets turn to mud. The mayor has asked the class to propose
different ways of paving the roads so that a person can get from any
one location to any other location on paved roads, but so that the
fewest number of roads possible are paved.