THE FIRST FOUR STANDARDSThe First Four Standards - Grades 5-6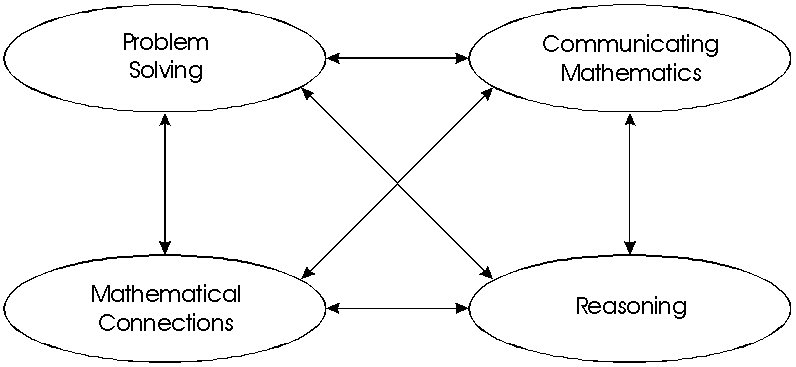
OverviewBy grades 5-6, students have mastered the basics of problem solving, communication, mathematical connections, and reasoning, and can apply these with reasonable facility to familiar topics. They are ready to consider more complex tasks in each of these areas as well as to apply their skills to more advanced mathematical topics such as probability, statistics, geometry, and rational numbers. Students in grades 5 and 6 should have experiences with a wide variety of problem-solving situations. Some of these should be process problems, in which the strategies students use are of more interest than the solution. For example: The Boys' Club held its annual carnival last weekend. Admission to the carnival was $3 for adults and $2 for children under 12. Total attendance was 100 people and $232 was collected. How many adults and how many children attended the carnival? (Kroll & Miller, 1993, p. 60) Charles & Lester (1982) recommend that students first discuss a problem as a whole class, focusing on understanding the problem and discussing possible strategies to use in solving the problem. While students are working on the problem, the teacher should observe and question students, offering hints or problem extensions as needed. After the students have solved the problem, they should show and discuss their solutions and relate the problem to others previously solved. For example, the problem above is similar in structure to the one involving pigs and chickens that was discussed in the K-12 Overview. Fifth- and sixth-graders should apply their improved communication skills to the new mathematics they are learning in order to help them better understand the concepts and procedures and to help their teachers better assess the students' understanding. Students should not only talk with each other in pairs, small groups, and as a class, they should also use mathematical symbols and language and draw pictures, diagrams, and other visual representations. Writing assignments may include keeping a journal or log, writing about mathematical concepts or procedures, or explaining how they solved a problem. Students in the middle grades have a wider range of mathematical connections to address than doyounger students. Within mathematics, multiple representations and patterns and generalizations are particularly important. For example, students might consider the numbers in the table below, looking for patterns and trying to develop a generalization (rule) that describes how the numbers are related.
They should consider not only the number sentence y = 3x that describes this pattern but also the verbal rule y is three times as big as x and the graph, which involves a straight line. Such activities not only develop communication skills, they also address patterns, numerical operations, and algebra. Students in grades 5 and 6 also apply mathematics to other subject areas and to real life. Social studies offers many opportunities for using data analysis and discrete mathematics, while art activities require the application of geometry. In science, students should observe and experiment with scientific phenomena and then summarize their observations using graphs, symbols, and geometry; they should translate the patterns they observe into mathematical terms. Following are several examples: Students might compare the amount of bounce that results from dropping a ball from various heights, develop a rule relating the height of bounce to the height of the drop, and use the rule to predict how high the ball will bounce from any given height. They might repeat the activity for a variety of different balls. Students might learn about how numbers are used as rates by having them measure the distance a toy car goes down an inclined ramp and the amount of time it takes, and then compute the speed. The study of angles might be related to reflections of light in a mirror or the construction of sundials, students might use graphs and charts concerning relative humidity or wind chill, they might examine magnification as a real-world context for multiplication, they might connect volume to studying about water or density, or they might use pulse rates or the mean temperature or rainfall as examples of averaging. Each of these activities demonstrates for students the usefulness of mathematics in learning about and doing science. Students in fifth and sixth grade continue to develop their basic reasoning skills. Much emphasis at these grade levels should be placed on inductive reasoning in which students look for patterns, make and test conjectures, and form generalizations based on their observations. Their ability to use deductive reasoning - to use logic and justify conclusions - is enhanced at these grade levels by the teacher's frequent use of this type of reasoning. For example: A square is a kind of rectangle. A rectangle is a kind of parallelogram. So a square is a kind of parallelogram. Students in the middle grades must be encouraged constantly to use their reasoning skills not only in mathematics class but also in other subjects and in their daily lives. Only in this way will they come to recognize the power of mathematical reasoning. As fifth- and sixth-graders expand their understanding of mathematics to include more advanced topics, they also expand their understanding of problem solving, communication, mathematical connections, and reasoning. They apply these skills to more difficult problems concerning topics they have already studied and to problems involving new mathematical concepts and procedures. They further use these skills to gain a better understanding of new ideas. References
On-Line Resources
The First Four Standards - Grades 5-6Vignette - Pizza PossibilitiesStandards: In addition to The First Four Standards, this vignette highlights Standards 8 (Numerical Operations), 11 (Patterns), and Discrete Mathematics (14). The problem: In a multi-aged group of fifth- and sixth-graders, the teacher posed this problem. Pizza Shack has asked us to help design a form to keep track of certain pizza choices. They offer a cheese pizza with tomato sauce. A customer can then select from the following toppings: pepperoni, sausage, mushrooms, and onions. How many different choices for pizza does a customer have? List all the possible choices. Find a way to convince each other that you have accounted for all the possible choices. The discussion: To check for understanding, the teacher had various students restate the problem. Students began the discussion thinking that there were only 4 choices. One student suggested that there could be a pizza with both pepperoni and sausage. Students then realized the difficulty of the problem. There was a question about whether a pizza with no toppings was allowed. Students brainstormed about ways to solve the problem. Some suggestions were: draw pictures, make a list, make a chart, use cubes of different colors to represent the different toppings, and use letters or numbers to represent each topping. Before the groups began to solve the problem, the teacher had students predict and record the number of possible choices. Solving the problem: Students worked in pairs for 15 to 20 minutes. Some groups had divided the work, with one student doing the 1- and 2-topping pizzas and the other the 3- and 4-topping pizzas. Others did the work separately and then compared their results. Still others had one person use cubes to show each combination as the other person recorded the combinations. Students kept track of the different kinds of pizzas in several ways.
Summary: Pairs of students reported to the class about how they solved the problem, and they compared their predictions with their actual results. They had some success giving convincing arguments, mostly relying on well-organized listing procedures. One pair of students suggested that they knew their solution was correct because it was part of the following pattern which involves powers of 2: if no toppings are available, there is only one pizza; if one topping is available, there are two possible pizzas; if two toppings are available, there are four possible pizzas; if three toppings are available, there are eight possible pizzas; and if four toppings are available, there are sixteen possible pizzas. With each extra topping, they correctly reasoned, the number of possibilities doubled, since each pizza on the previous list could now also be made with the additional topping. They confirmed their reasoning by constructing a chart like that above with 16 different rows, each row representing one possible pizza. The First Four Standards - Grades 5-6Vignette - Two-Toned TowersStandards: In addition to the First Four Standards, this vignette highlights Standards 7 (Geometry), 8 (Numerical Operations), 11 (Patterns), 13 (Probability and Statistics), and 14 (Discrete Mathematics). The problem: The same multi-aged group which worked on the pizza problem was challenged with this towers problem several weeks later. Your group's task is to build as many towers as you can that are 4 cubes tall and that use no more than 2 colors. Then you are to convince each other that there are no duplicates and none has been omitted. The discussion: Students questioned the meaning of "no more than 2 colors." Some thought that each tower must have 2 colors, other thought that towers of 1 color were also allowed. After some discussion, students agreed, for this problem, to build towers with 1 or 2 colors. The teacher then asked two volunteers to build two towers each - one that satisfied the conditions of the problem and the other that did not. Students discussed each tower, and decided which ones were appropriate. Some students wondered if they had to build the towers, or if they could just draw and label the towers. The group decided that not actually building the towers was okay, as long as each student kept a permanent record of the towers that he "built." Solving the problem: Students worked in pairs or other small groups to begin building the towers. In most groups, at least one person felt more comfortable actually building the towers, rather than relying on drawing the towers. As the groups worked, the teacher stopped at each group, and encouraged students to talk about how they knew when all the towers were made and how they knew there were no duplicates. Some students working with red and blue cubes were very organized, building towers in this order: RRRR, BRRR, RBRR, RRBR, RRRB, and so on. Others worked very haphazardly, and did not organize their towers until they were all made. Still others used an "opposites" approach, making the RRRB tower followed by BBBR, RBBR followed by BRRB, and so on. Summary: Students used their solutions to the problem as a focal point for their reports to the class. All of the students agreed that there were 16 towers and were able to convince their classmates by using some variation of the organized list strategy. Then, one student suggested that somehow the pizza problem and the towers problem were alike. Students grappled with the idea for a few minutes. Then the teacher suggested that they list the things that were alike about the problems. Their list included these ideas: there were 4 toppings in the pizza problem and 4 blocks in each tower; 0 toppings was like a tower of all one color and 4 toppings was like a tower of all the other color. After more discussion, students realized that they could better match up the two problems if they put the toppings in a specific order, like pepperoni, mushrooms, sausage, and onions. Then if you ordered a pizza with only pepperoni and mushrooms, it would be like saying "yes, yes, no, no" to the four toppings; and that was like building a tower which was "red, red, blue, blue." A pizza with pepperoni and sausage, or "yes, no, yes, no", would match up to the tower of "red, blue, red, blue." As the discussion went on, students went back to their problem-solving groups to record the connections between the two problems. At the end of the class, the teacher explained that both of these problems belong to an area of mathematics called combinatorics, which deals with problems involving combinations and is used in analyzing games of chance. The First Four Standards - Grades 5-6IndicatorsThe cumulative progress indicators for grade 8 for each of the First Four Standards appear in boldface type below the standard. Each indicator is followed by a brief discussion of how the preceding grade-level vignettes might address the indicator in the classroom in grades 5 and 6. The Introduction to this Framework contains three vignettes describing lessons for grades 5-8 which also illustrate the indicators for the First Four Standards; these are entitled The Powers of the Knight, Short-circuiting Trenton, and Mathematics at Work.
Building upon knowledge and skills gained in the preceding grades, experiences in grades 5-6 will be such that all students: 4*. Pose, explore, and solve a variety of problems, including non-routine problems and open-ended problems with several solutions and/or solution strategies.
5*. Construct, explain, justify, and apply a variety of problem-solving strategies in both cooperative and independent learning environments.
6*. Verify the correctness and reasonableness of results and interpret them in the context of the problems being solved.
7*. Know when to select and how to use grade-appropriate mathematical tools and methods (including manipulatives, calculators and computers, as well as mental math and paper-and-pencil techniques) as a natural and routine part of the problem-solving process.
8*. Determine, collect, organize, and analyze data needed to solve problems.
10. Use discovery-oriented, inquiry-based, and problem-centered approaches to investigate and understand mathematical content appropriate to the middle grades.
11. Recognize, formulate, and solve problems arising from mathematical situations, everyday experiences, and applications to other disciplines.
12. Construct and use concrete, pictorial, symbolic, and graphical models to represent problem situations and effectively apply processes of mathematical modeling in mathematics and other areas.
13. Recognize that there may be multiple ways to solve a problem, weigh their relative merits, and select and use appropriate problem-solving strategies.
14. Persevere in developing alternative problem-solving strategies if initially selected approaches do not work.
Building upon knowledge and skills gained in the preceding grades, experiences in grades 5-6 will be such that all students: 1*. Discuss, listen, represent, read, and write as vital activities in their learning and use of mathematics.
2*. Identify and explain key mathematical concepts, and model situations using oral, written, concrete, pictorial, and graphical methods.
3*. Represent and communicate mathematical ideas through the use of learning tools such as calculators, computers, and manipulatives.
4*. Engage in mathematical brainstorming and discussions by asking questions, making conjectures, and suggesting strategies for solving problems.
5*. Explain their own mathematical work to others, and justify their reasoning and conclusions.
6. Identify and explain key mathematical concepts and model situations using geometric and algebraic methods.
7. Use mathematical language and symbols to represent problem situations, and recognize the economy and power of mathematical symbolism and its role in the development of mathematics.
8. Analyze, evaluate, and explain mathematical arguments and conclusions presented by others.
Building upon knowledge and skills gained in the preceding grades, experiences in grades 5-6 will be such that all students: 1*. View mathematics as an integrated whole rather than as a series of disconnected topics and rules.
2*. Relate mathematical procedures to their underlying concepts.
3*. Use models, calculators, and other mathematical tools to demonstrate the connections among various equivalent graphical, concrete, and verbal representations of mathematical concepts.
4*. Explore problems and describe and confirm results using various representations.
8. Recognize and apply unifying concepts and processes which are woven throughout mathematics.
9. Use the process of mathematical modeling in mathematics and other disciplines, and demonstrate understanding of its methodology, strengths, and limitations.
10. Apply mathematics in their daily lives and in career-based contexts.
11. Recognize situations in other disciplines in which mathematical models may be applicable, and apply appropriate models, mathematical reasoning, and problem solving to those situations.
Building upon knowledge and skills gained in the preceding grades, experiences in grades 5-6 will be such that all students: 2*. Draw logical conclusions and make generalizations.
3*. Use models, known facts, properties, and relationships to explain their thinking.
5*. Analyze mathematical situations by recognizing and using patterns and relationships.
6. Make conjectures based on observation and information, and test mathematical conjectures and arguments.
7. Justify, in clear and organized form, answers and solution processes in a variety of problems.
8. Follow and construct logical arguments, and judge their validity.
9. Recognize and use deductive and inductive reasoning in all areas of mathematics.
10. Utilize mathematical reasoning skills in other disciplines and in their lives.
11. Use reasoning rather than relying on an answer-key to check the correctness of solutions to problems.
* Reference is made here to Indicators 4, 5, 6, 7, and 8, which are also listed for grade 4, since the Standards specify that students demonstrate continued progress in these indicators. * Reference is made here to Indicators 1, 2, 3, 4, and 5, which are also listed for grade 4, since the Standards specify that students demonstrate continued progress in these indicators. * Reference is made here to Indicators 1, 2, 3, and 4, which are also listed for grade 4, since the Standards specify that students demonstrate continued progress in these indicators. * Reference is made here to Indicators 2, 3, and 5, which are also listed for grade 4, since the Standards specify that students demonstrate continued progress in these indicators. |