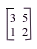 as a key to encode the message MATH.
as a key to encode the message MATH.
The Hill cipher is a type of substitution cipher that uses matrix multiplication for both the message and the key.
Enter your message in a matrix M of dimensions r*c using filler at the end if necessary. Use an invertible r*r matrix E as your key. The determinant of E must be relatively prime to the modulus m of you alphabet. To encode multiply the matrix M on the left by E. To decode multiply the product on the left by the inverse of your key: E^-1 (EM)=M. Don't convert modulo m until you are ready to recover your plaintext.
Ex) Use the matrix 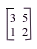 as a key to encode the message MATH.
as a key to encode the message MATH.
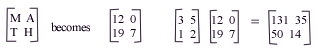
This can be sent as 131 35 50 14. Your recipient will decode the message by putting the message in matrix form and then multiply by the inverse of the key:
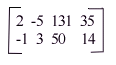 Note: To encode and decode, the key must be on the left.
Note: To encode and decode, the key must be on the left.
1. What is the product of E and E^-1?
2. Use a 2*8 matrix and the key above to send the message MATH IS DISCRETE. Use Q as filler.
3. Use the key  to send the message WHAT DOES MATRIX MEAN.
to send the message WHAT DOES MATRIX MEAN.
4. Create a 3*3 key to encrypt NO HOMEWORK TONIGHT.
5. Send a message to a friend using your 3*3 key.
6. Share messages with a friend using a common key.