Query Certificate Managers

  A QCM program defines a database and resides at a node in a computer network. Each program is associated with a unique principal ; principals are traditionally the entities that take part in protocols by signing and exchanging messages. Conceptually, the principal of a QCM program accepts queries from other principals, supplies the queries as input to the QCM program, and returns the result after signing it. Following standard practice [4,7], a QCM principal is actually a public key. A principal signs documents using its associated secret key, and the signature can be verified using only the signed document and the principal itself.

The principal of a QCM program also serves as a name for the database defined by the program. By referring to remote principals, a QCM database can be defined in terms of remote QCM databases. Principals are thus used for both authentication and data distribution in QCM. Our first example, content filtering , illustrates these ideas.

Content filtering prevents web pages with objectionable content from being displayed on a web browser. We show how QCM can implement content filtering based on page ratings provided by rating services. There are four principals: a page server, s ; two rating services, r1 and r2 ; and a browser, b . The rating services maintain databases associating a rating (G, PG, etc.) with the cryptographic hash of a page. Conceptually, these databases are tables:

$$\begin{array}[t] {cc} \multicolumn{2}{c}{r1.\textbf{ratings... ... h4 & PG\\ h5 & PG\\ \multicolumn{2}{c}{\vdots} \end{array}$$

The table $r1.\textbf{ratings}$ is controlled by r1 and is completely independent of the second table, $r2.\textbf{ratings}$. For instance, r1 and r2 do not have to agree on the rating for a page, and do not have to rate the same pages.

The browser b can define a ratings database of its own by the following QCM program:

$$\begin{array} {l} \textbf{ratings}= r1.\textbf{ratings}\cap... ...a_{\textrm{\scriptsize rating}=G}\textbf{ratings}) \end{array}$$

This defines two tables, $b.\textbf{ratings}$ and $b.\textbf{ok}$, using relational algebra expressions, which are the basis of QCM. The table $b.\textbf{ratings}$ is defined to be the intersection of the two remote ratings databases:

$$\begin{array}[t] {cc} \multicolumn{2}{c}{b.\textbf{ratings}... ...e h1 & G\\ h4 & PG\\ \multicolumn{2}{c}{\vdots} \end{array}$$

The second definition, for $b.\textbf{ok}$, is more complicated. The selection operator, $\sigma_{\textrm{\scriptsize rating}=G}$, constructs a table by starting with $b.\textbf{ratings}$, and discarding all rows not rated G. The projection operator, $\pi_{\textrm{\scriptsize hash}}$, discards all columns except for $\textrm{hash}$. The result is a table of hashes with G ratings, which the browser is willing to display:

$$\begin{array} {c} b.\textbf{ok}\\ \textrm{hash}\\ \hline h1\\ \vdots \end{array}$$

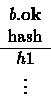
Now, the tables $b.\textbf{ratings}$ and $b.\textbf{ok}$ may be very large, because $r1.\textbf{ratings}$ and $r2.\textbf{ratings}$ may be large. Therefore, the actual tables are not materialized at b , and instead are fetched as needed. However, our semantics will guarantee that the application programmer can think of them as tables residing at b .

The QCM program can execute in a number of ways. In the first way, the browser obtains a page, h , from the server s . It then needs to check whether the page should be displayed, that is, whether h is in the table $b.\textbf{ok}$. It does this by asking QCM to evaluate a relational algebra query:

$$\sigma_{\textrm{\scriptsize hash}=h}\textbf{ok}.$$

This will construct a new table consisting of the rows of $\textbf{ok}$ in which the hash is h : either the table will be empty (and the browser will not display the page), or it will have a single row, h (and the browser will display the page). The execution of QCM can be explained by algebraic reasoning. Beginning with the query, we simply fill in the definition of $\textbf{ok}$, and then $\textbf{ratings}$:

$$\begin{eqnarray*} \sigma_{\textrm{\scriptsize hash}=h}\textbf{ok} & = & \sigma... ...iptsize rating}=G}(r1.\textbf{ratings}\cap r2.\textbf{ratings})))\end{eqnarray*}$$

At this point, QCM could request the entire $r1.\textbf{ratings}$ and $r2.\textbf{ratings}$ databases and finish evaluating the query. However, these databases are likely to be large, so further algebraic reasoning is used:

$$\begin{eqnarray*} \sigma_{\textrm{\scriptsize hash}=h}\textbf{ok} & = & (\pi_{... ...size hash}=h,\textrm{\scriptsize rating}=G} r2.\textbf{ratings}))\end{eqnarray*}$$

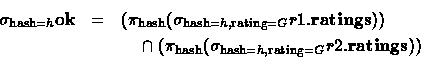
That is, it is more efficient to throw away rows and columns at r1 and r2 , rather than at b .

Now, QCM will automatically send the query $(\pi_{\textrm{\scriptsize hash}}(\sigma_{\textrm{\scriptsize hash}=h,\textrm{\scriptsize rating}=G}r1.\textbf{ratings}))$ to r1 ; the response will be small, at most one row. The responses from r1 and r2 can be combined to form the answer to the original query in the obvious way.

What we have just described is standard distributed database query evaluation. But note that it is quite expensive: to view one page, three queries and three responses were required. For efficiency, the server s might arrange to have r1 and r2 give it certificates for its page h . We write such certificates in the form

$$\begin{array} {l} \textbf{$r1$\space says $r1.\textbf{ratin... ...langle\textrm{hash}:h,\textrm{rating}:G\rangle\}$} \end{array}$$

These are documents signed by r1 and r2 , asserting that a row with hash h and rating G appears in their respective ratings databases. (The digital signature is implicit in our certificate notation.)

In this scenario, when the browser asks s for the page h , s will send along the two ratings certificates as well. The browser will submit the certificates to QCM along with its query, $\sigma_{\textrm{\scriptsize hash}=h}\textbf{ok}$. In this case, QCM will carefully examine the certificates, and, if everything checks out, will be able to evaluate the query without exchanging messages with r1 and r2 . This sort of computation is not standard in databases.

We feel it is vital to support both of these computations. Clearly the second computation can be more efficient, but it also requires cooperation between s , r1 , and r2 . If the rating services do not give s a good rating for its pages, it may not be willing to carry their certificates. For this reason, other filtering proposals, such as PICS [8], also specify that both ways of obtaining ratings should be possible. The advantage of our system is that it covers all possibilities, without forcing the programmer to write code for each case. If both ratings certificates are provided by s , neither r1 nor r2 is queried by QCM; if neither certificate is provided, both r1 and r2 will be queried; and if only r1 's certificate is provided, then only r2 will be queried. In each of these cases, the same QCM program (above) is used.

Notice that we did not give QCM programs for $r1.\textbf{ratings}$ and $r2.\textbf{ratings}$. In fact, they need not be implemented by QCM programs; for example, they may be stored in proprietary databases. All that is required is that r1 and r2 understand the message format of QCM database queries and responses. Although complete databases can be programmed entirely in QCM, we think that the authenticated integration of existing databases into the network will be one of the most important services provided by QCM.

Take, for example, the problem of public key distribution . VeriSign [9] is a company that issues digital IDs , certificates that associate a public key and an e-mail address with a name. There are several classes of IDs, and the class of an ID reflects how much trust should be put in the binding of key to name. For example, Class 3 IDs must be requested in person, with proper identification, while Class 1 IDs can be requested by e-mail. To integrate a database of digital IDs using QCM, we simply regard it as a relation with a particular schema, e.g.,

$$\textit{VeriSign}.\textbf{IDs}(\textrm{name},\textrm{key},\textrm{e-mail},\textrm{class})$$

Using QCM, a programmer can define a public key directory as the union of some locally-known bindings, as well as trustworthy entries from VeriSign's database of IDs:

$$\textbf{pkd}= \begin{array}[t] {@{}l@{}} \{\langle\textrm{... ...size class}\gt 1} \textit{VeriSign}.\textbf{IDs}) \end{array}$$

The expression on the right defines a relation containing an entry for Bob, as well as other entries derived from VeriSign's database. We use $\sigma_{\textrm{\scriptsize class}\gt 1}$ to discard Class 1 IDs in VeriSign's database as untrustworthy, and $\pi_{\textrm{\scriptsize name},\textrm{\scriptsize key},\email}$ to discard the $\textrm{class}$ column from the resulting table. Thus $\textbf{pkd}$ is a table with columns labeled $\textrm{name}$, $\textrm{key}$, and $\textrm{e-mail}$.

The programmer can query the local pkd for keys. For example, to obtain Alice's keys (she may have more than one), the programmer asks $\pi_{\textrm{\scriptsize key}}(\sigma_{\textrm{\scriptsize name}=\textrm{\scriptsize Alice}}\textbf{pkd})$. By combining this query with the definition of pkd, and using algebraic reasoning, QCM derives a query to ask VeriSign for the appropriate certificates:

$$\sigma_{\textrm{\scriptsize name}=\textrm{\scriptsize Alice},\textrm{\scriptsize class}\gt 1}\textit{VeriSign}.\textbf{IDs}$$

Notice that we do not bother to request Class 1 IDs. VeriSign's response will be processed to construct the table of Alice's keys, just as we described in the filtering example. Alternately, QCM can be used to validate a purported ID for Alice: if the ID is submitted to QCM along with the same query, QCM will examine its signature and use it to evaluate the query, short-circuiting any message to VeriSign.

As a final example, access control lists (ACLs) can be programmed in QCM:

$$\textbf{friends}= \{p,q\} \cup p.\textbf{friends}$$

This is a QCM definition of a database, $\textbf{friends}$, that includes the principals p , q , and the principals in the remote database $p.\textbf{friends}$. Sets of principals like $\textbf{friends}$ can be used as ACLs to protect resources in the network: requests will be granted only if signed by a principal in the ACL.