A key theorem

We obtain an extremely specialised theorem that applies to authentication properties on this specific description NET of the network. This theorem is at the heart of the proof strategy presented in this paper. It provides a sufficient list of conditions whose achievement guarantees that NET $\mbox{ \bf sat }$ $\mbox {\tt $T$\space authenticates $R$}$.

Theorem 1

 $\rho : MESSAGE \rightarrow \mbox{\Bbb Z}$ is such that

C1:

$\forall m \in INIT . \rho(m) \gt 0$

C2:

$(\forall m' \in S . \rho(m') \gt 0)) \land S \vdash m \Rightarrow\rho(m) \gt 0$

C3:

$\forall m \in T . \rho(m) \leq 0$

C4:

$\forall i . (USER_i \parallel[R] \mbox{ \em Stop }\mbox{ \bf sat }~~\mathrel{\mathsf{maintains}} \rho )$

then $NET \parallel[R] \mbox{ \em Stop }\mbox{ \bf sat }tr$ $\mbox{$\mid$\hspace{-.037in}\small\`{}}$ $T = \langle \rangle$

The rank function $\rho$ is intended to have positive value on all messages which can be generated by some agent (including the enemy) during a run of the protocol, when all messages in the set R are prevented from occurring. The intention is to show that this restriction on R means that no event from T can occur, and hence by Lemma 1 that $T \mathrel{\mathsf{authenticates}}R$. Conditions C1 and C2 together mean that if the enemy only ever sees messages of positive rank, then he can only ever generate messages of positive rank.

Condition C4 states that the same is true for the users of the network (when restricted on R ): they never output a message of non-positive rank unless they previously received such a message. The specification $\mathrel{\mathsf{maintains}}\rho$ is defined as:

$$\begin{array} {l} \mathrel{\mathsf{maintains}}\rho(tr) \stac... ...forall m \in (tr \Downarrow trans) : \rho(m) \gt 0) \end{array}$$

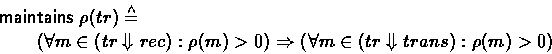
If every message received on rec has positive rank, then so does every message sent out on trans .

The predicate ``$\rho(m) \gt 0$'' can therefore be seen as describing an invariant: at every stage of the protocol's execution when R is suppressed, it must hold of the next message. Since C3 states that it does not hold for any message in T , this means that no message in T can ever be generated.

The problem for any particular protocol, and a particular authentication property expressed in terms of R and T , is to find an appropriate rank function $\rho$ which makes C1 to C4 all true, and to verify this fact.