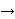 V(H) is a homomorphism from G to H if
f(x)f(y) is an edge of H for every edge xy of G.)
V(H) is a homomorphism from G to H if
f(x)f(y) is an edge of H for every edge xy of G.)
- First Meeting
- Dates: December 2 -6, 2002
Location: Samalova chata, Nova Louka, Czech Republic- Second Meeting
- Dates: April 6 - 7, 2004
Location: Alfred Renyi Institute, Budapest, Hungary- Third Meeting
- Dates: November 7 - 9, 2005
Location: DIMACS Center, CoRE Building, Rutgers University
DIMACS/DIMATIA/Renyi Tripartite Partnership
The intersection of combinatorics and statistical physics has been an
area of great activity over the past few years, fertilized by an
exchange not only of techniques but of objectives. This
interconnection was featured in a joint DIMACS-DIMATIA workshop on
this topic. (See http://dimacs.rutgers.edu/Workshops/Graph-Morph/)
Spurred by computing theorists interested in approximation algorithms,
statistical physicists and discrete mathematicians have
found a wealth of common ground in probabilistic
combinatorics. Close connections between percolation and random
graphs, between graph homomorphisms and hard-constraint models, and
between slow mixing and phase transition, have led to new results and
new perspectives. Of special interest is the use of these connections
in understanding typical, as opposed to extremal, behavior of
combinatorial phenomena such as graph coloring and
homomorphisms. (Recall that given graphs G and H, a mapping f:
V(G) 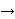 V(H) is a homomorphism from G to H if
f(x)f(y) is an edge of H for every edge xy of G.)
V(H) is a homomorphism from G to H if
f(x)f(y) is an edge of H for every edge xy of G.)
Any ``nearest neighbor'' system of statistical physics can be interpreted as a space of graph homomorphisms - for example, homomorphisms to the two-node graph with one edge and one loop correspond to the ``hard-core lattice gas model'' and to random independent sets. Given the set of homomorphisms from a (possibly infinite) graph G to a graph H, so-called H-colorings, when do we see long range order? When does changing the homomorphism site by site (heat bath) yield rapid mixing, or even eventual mixing? The special case of proper colorings (corresponding to the anti-ferromagnetic Potts model at zero temperature) is especially interesting to graph theorists (see [12] but more general notions of graph colorings may also yield some intriguing new questions.
In [31], Winkler defined a purely combinatorial, non-probabilistic notion of long range order for graph homomorphisms, and studied when this arises in maps from a Cayley tree to a graph H with given chromatic number. This work was part of a plan to study combinatorial versions of concepts from statistical physics, and in particular to link graph properties which view a graph as the target of a homomorphism to others in which it is the source, and we shall pursue this plan. Colorings of trees have been a special topic of interest in this field. During the DIMACS Special Focus on Discrete Probability (co-sponsored by the Institute for Advanced Study), Graham Brightwell and Peter Winkler [12] used random 3-colorings of binary trees as models of the phenomena studied in statistical mechanics. They found a random 3-coloring of a binary tree (subject to the condition that no red point may be adjacent to a green one) as an illustration that such colorings can exhibit phase transitions akin to the phase transitions exhibited by physical systems. Their example showed a ``phase'' in which green is favored over red even though the local conditions are the same for those two colors. For more general discussion of graph-theoretical models of phase transitions, see [10, 11]. In more recent work, Brightwell and Winkler [13] noted that, when considering probability measures on the set of H-colorings of an infinite graph G, one of the simplest scenarios is when H is a complete unlooped graph and G is a regular tree. They concentrated on a particularly nice class of Gibbs measures which are invariant under parity-preserving automorphisms of the tree and determined when more than one such measure exists. They also analyzed the question of when there is a unique Gibbs measure, and considered extensions to other graphs H. We would like to extend this type of work in this working group.
In other relevant work on colorings, Borgs [6] considered random H-colorings of rectangular subsets of the hypercubic lattice, with separate weights for each color. For a large class of graphs H, he showed that the weights can be chosen such that all quasi-local Markov chains have exponentially slow mixing. For most such H he also showed that it is possible to find (different) weights for which the Gibbs measure has exponentially fast spatial mixing. Generalizing the results to other classes of graphs remains an interesting direction of research which we will pursue.
In other relevant work on phase transitions, Borgs, Chayes, and Pittel [7] studied the optimum partitioning problem, a canonical NP-complete problem of combinatorial optimization, and showed that the model has a phase transition and established the behavior of the model near the transition. In particular, they showed that the phase transition is discontinuous or ``first-order,'' in contrast to the phase transitions established in other combinatorial models such as the random graph and the 2-satisfiability problem. They discussed recent suggestions that the order of the phase transition may be related to the hardness of the problem and this working group will continue to investigate this suggestion.
The work of the working group on Graph Colorings and Generalizations is also relevant here. Specifically relevant is work on ``list homomorphisms'' [18, 19]. Given a fixed target graph H and an input graph G together with lists S(x) from V(H), x in V(G), is there a homomorphism f:G rightarrow H such that each f(x) is in S(x)? How many such homomorphisms are there? Hell and Nesetril have obtained preliminary results giving algorithms for these questions and some generalizations, and we shall pursue this investigation in this working group. The earlier work of Gallucio, Hell and Nesetril [17] on ordinary H-colorings should be helpful here.
A second major area of interest for this group concerns combinatorial geometry, in particular finite geometries, geometric graphs, and problems involving point sets in the plane. A finite geometry (finite projective plane) P of order q is a family of q2+q+1 subsets (called lines) of a base set of size q2+q+1 (called the set of points), where each line has q+1 points, and any two of the lines have exactly one point in common. Finite geometries is an area of combinatorics closely related to combinatorial designs. This area has many intriguing open problems and applications in cryptography, design of computer and communication networks, software testing, storage in disk arrays, signal processing, sports scheduling, group testing, and clone screening in molecular biology. (See Colbourn, Dinitz and Stinson [14] and Stinson [25] for a discussion of these applications of finite geometries and combinatorial designs.)
One area we propose to study concerns blocking sets. A subset B of the points in a finite geometry is called a blocking set if both B and its complement $\barB$ intersect all lines. A classical question of Erdós asks for the existence of an absolute constant C such that in any finite projective plane there exists a blocking set intersecting every line in no more than C points. There are many related results, but none of them solves this problem. For Galois planes PG(2, q), q = pr, p prime, there are blocking sets intersecting all lines in no more than p+1 points (see [8]). In particular, for planes of prime order q = p there is no known o(p) bound. Computational evidence (see [4]) seems to suggest that the true order of magnitude may be log p, rather than a constant. We shall try to determine if this is indeed the case.
Another exciting area concerns defining sets. A subset D of the lines of a finite projective plane is called a defining set if no other projective plane can contain D as a subfamily (i.e. D can be uniquely extended to a plane by adding further lines). Recent results on the size of defining sets in PG(2,q) using a random construction suggest that further improvements are possible. Combining the approach of Boros and Szonyi [9] with a result of Kahn [20], we hope to show that PG(2,q) allows defining sets of size O(q).
This working group will interact with the working group on Extremal Combinatorics on a number of topics, most specifically on group testing. The connections among group testing, combinatorial designs, and finite geometries are discussed in [14, 25].
A geometric graph is a graph drawn in the plane so that the vertices are represented by points in general position and the edges are represented by straight line segments connecting the corresponding points. We shall consider Turán-type problems for geometric graphs. One problem is to find the maximum number ck(n) of edges in a geometric graph on n vertices with no k pairwise crossing edges. Agarwal, et al. [1] proved that c3(n) = O(n) and Valtr [29, 30] proved that ck(n) = O(n log n). However, the question of whether or not ck(n) = O(n) for k > 3 remains open and we shall investigate it. One promising approach to this problem is via generalized Davenport-Schinzel sequences, which were used to prove the O(n log n) result. (See [28] for a survey of Davenport-Schinzel sequences.)
A related problem is to find dk(n), the maximum number of edges in a geometric graph on n vertices with no k pairwise disjoint edges. In contrast to the case of ck(n), it is known that dk(n) = O(n). The first proof of this for any fixed k > 2 was in [23], where it was proved that dk(n) < (k-1)4n. This was later asymptotically improved to dk(n) < ckk3n in [27] and dk(n) < ckk2n in [26]. The best known lower bound on dk(n) (roughly 3/2(kn) can also be found in [27]. We would like to improve on this bound.
We will also investigate similar problems for parallel edges. Two edges in a geometric graph are parallel if they are disjoint and the convex hull of their union is a convex quadrilateral. We will study pk(n), the maximum number of edges in a geometric graph on n vertices with no k pairwise parallel edges. In [29], it is shown that pk(n) = O(n). We shall work on upper and lower bounds for this parameter.
A hyperplane 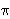
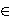 Rd ``bisects'' a set S of n points in Rd
if at most n/2 points lie in the open halfspaces determined by
Rd ``bisects'' a set S of n points in Rd
if at most n/2 points lie in the open halfspaces determined by
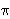 . The ham sandwich theorem states that there is a hyperplane
. The ham sandwich theorem states that there is a hyperplane
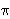
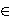 Rd which simultaneously bisects d given sets
S1,...,Sd in Rd. Recently several interesting extensions and
generalizations have been presented
[3, 5, 21]). Two proofs were given of the following
conjecture of Kaneko and Kano: Given points of k given colors in
general position in the plane, kni points of color i, there
is a partition of the plane into k disjoint convex subsets, and in
each subset, ni points of color i (k=2 is the ham-sandwich
theorem). Bárány and Matou\v{s}ek proved that
points of k=3 different colors in the plane may be simultaneously
bisected by a ``chain'' consisting of k-1=2 ``segments'' (halflines
emanating from a single point). The case 0k=2 is the usual ham-sandwich
theorem; the chain is one line. We will study
these and other recent generalizations, and try to develop new
ones. We will also consider related algorithmic questions and in
particular the complexity of computing these cuts.
Rd which simultaneously bisects d given sets
S1,...,Sd in Rd. Recently several interesting extensions and
generalizations have been presented
[3, 5, 21]). Two proofs were given of the following
conjecture of Kaneko and Kano: Given points of k given colors in
general position in the plane, kni points of color i, there
is a partition of the plane into k disjoint convex subsets, and in
each subset, ni points of color i (k=2 is the ham-sandwich
theorem). Bárány and Matou\v{s}ek proved that
points of k=3 different colors in the plane may be simultaneously
bisected by a ``chain'' consisting of k-1=2 ``segments'' (halflines
emanating from a single point). The case 0k=2 is the usual ham-sandwich
theorem; the chain is one line. We will study
these and other recent generalizations, and try to develop new
ones. We will also consider related algorithmic questions and in
particular the complexity of computing these cuts.
One of the main features of research in contemporary science in general and discrete mathematics in particular is the strong interrelation of parts of mathematics long thought to be unrelated. Thus the combinatorial methods in statistical physics are based in invariant theory and algebraical techniques (Tutte polynomials and homomorphisms) while some of the most efficient structures in combinatorial geometry and combinatorics are achieved by means of advanced algebraic geometry. This is our motivation for combining the two at-first-blush different topics of combinatorial geometry and homomorphisms/statistical physics in this one working group. To tie these topics together, we shall investigate the uses of combinatorial methods in algebraic geometry and the uses of algebraic geometry methods in combinatorics. The work will build in part on a DIMACS workshop on Algorithmic and Quantitative Aspects of Real Algebraic Geometry in Mathematics and Computer Science held in March 2001 (see http://dimacs.rutgers.edu/archive/Workshops/Algorithmic/).
We mention some exciting recent developments in the application of elementary algebraic geometry to combinatorics, mostly to classical extremal problems. In his seminal paper [2], Alon proved a surprisingly powerful yet elementary nonvanishing theorem for polynomial functions on finite product sets in an affine space. Applications include results in additive number theory and existence theorems for regular subgraphs and graph colorings. Moreover, the approach allows a unified treatment of several known results which describe combinatorial properties in terms of ideals in polynomial rings. In [22], Kollár, Rónyai and Szabó used algebraic hypersurfaces to construct graphs with high edge density but without complete bipartite graphs as subgraphs. Recently, Elekes and Szabó [15, 16] studied 3-variate real polynomials which take few values on certain boxes of the form XxYxZ, where X,Y,Z are finite subsets of the reals. Drawing tools from the theory of algebraic curves, they established a structure theorem for such polynomials. These three research directions open new avenues in applying algebro-geometric tools to combinatorial problems which we intend to pursue, specifically the study of the ideals of infinite point sets other than complete direct products in order to obtain interesting nonvanishing theorems for novel combinatorial applications; modifications/extensions of the geometric construction behind the norm graphs, particularly, intersections of diagonal hypersurfaces or more general algebraic varieties in order to obtain interesting explicit constructions of extremal objects; and extensions to polynomials/rational functions involving more than three variables. This working group will also examine various topics that lie at the interface between the two disciplines of computational geometry and real algebraic geometry, topics such as construction and analysis of arrangements of algebraic surfaces, lower bound proofs, robust computations, and more. The contributions of real algebraic geometry to computational geometry are quite well known, but perhaps less well known are some interactions in the other direction, e.g., separating the `combinatorial' from the `algebraic' complexity of semialgebraic sets [24].
[1] Agarwal, P.K., Aronov, B., Pach, J., Pollack, R., and Sharir, M., ``Quasi-planar Graphs Have a Linear Number of Edges,'' Combinatorica, 17, (1997), 1-7.
[2] Alon, N., ``Combinatorial Nullstellensatz,'' Combin. Probab. Comput., 8, (1999), 7-29.
[3] Bárány, I., ``A Short Proof of Kneser's Conjecture,'' J. Comb. Th., A25, (1978), 325-326.
[4] Béres, L., and Illés, T., ``Computational Investigation of the Covering Number of Finite Projective Planes with Small Order,'' Alkalmaz. Mat. Lapok, 17, (1997), 397-411.
[5] Bespamyatnikh, S., Kirkpatrick, D., and Snoeyink, J., ``Generalizing Ham Sandwich Cuts to Equitable Subdivisions,'' Discrete and Comp. Geom., 24, (2000), 605-622.
[6] Borgs, C., ``On Mixing for Random H-Colorings of the Hypercubic Lattice,'' DIMACS-DIMATIA Workshop on Graphs, Morphisms and Statistical Physics, DIMACS, March 2001.
[7] Borgs, C., Chayes, J., and Pittel, B., ``A Phase Transition in the Optimum Partitioning Problem,'' DIMACS-DIMATIA Workshop on Graphs, Morphisms and Statistical Physics, DIMACS, March 2001.
[8] Boros, E., ``PG(2, ps), p >2 Has Property B(p+2),'' Ars Combinatoria, 25, 111-113.
[9] Boros, E., and Szonyi, T., ``On Partial Projective Planes,'' Technical Report, MO 11-86, CAI-HAS, SZTAKI, March 1986. (In Hungarian)
[10] Brightwell, G., and Winkler, P., ``Graph Homomorphisms and Phase Transitions,'' J. Comb. Th., B77, (1999), 415-435.
[11] Brightwell, G., and Winkler, P., ``Gibbs Measures and Dismantlable Graphs,'' J. Comb. Theory, B78, (2000), 141-169.
[12] Brightwell, G., and Winkler, P., ``Random Colorings of a Cayley Tree,'' preprint, Bell Labs, 2000.
[13] Brightwell, G., and Winkler, P., ``Proper Colorings of Regular Trees,'' DIMACS-DIMATIA Workshop on Graphs, Morphisms and Statistical Physics, DIMACS, March 2001.
[14] Colbourn, C.J., Dinitz, J.H., and Stinson, D.R., ``Applications of Combinatorial Design to Communications, Cryptography, and Networking,'' http://www.emba.uvm.edu/~dinitz/preprints.html
[15] Elekes, Gy., and Szabó, E., ``On Triple Lines and Cubic Curves,'' Combinatorica, to appear.
[16] Elekes, Gy., and Szabó, E., ``Triple Points of Circle Grids,'' Combinatorica, to appear.
[17] Galluccio, A., Hell, P., and Nesetril, J., ``The Complexity of H-coloring of Bounded Degree Graphs,'' KAM-DIMATIA Technical Report 99-416, 1999.
[18] Hell, P., ``List Homomorphisms,'' DIMACS-DIMATIA Workshop on Graphs, Morphisms and Statistical Physics, DIMACS, March 2001.
[19] Hell, P., and Nesetril, J., ``Counting List Homomorphisms and Graphs with Bounded Degree,'' KAM-DIMATIA Series Technical Report 2001-521, 2001.
[20] Kahn, J., ``On a Problem of Erdös and Lovász: Random Lines in a Projective Plane,'' Combinatorica, 12, (1992), 417-423.
[21] Kaneko, A., and Kano, M., ``Balanced Partitions of Point Sets in the Plane,'' Computational Geometry, 13, 1999, 253-261.
[22] Kollár, J., Rónyai, L., and Szabó, T., ``Norm Graphs and Bipartite Turán Numbers,'' Combinatorica, 16, (1996), 399-406.
[23] Pach, J., and Törocsik, J., ``Some Geometric Applications of Dilworth's Theorem,'' Discrete Comput. Geom., 12, (1994), 1-7.
[24] Sharir, M., ``What Can Computational Geometry and Real Algebraic Geometry Contribute to Each Other,'' DIMACS Workshop on Algorithmic and Quantitative Aspects of Real Algebraic Geometry in Mathematics and Computer Science, March 2001.
[25] Stinson, D.R., ``Combinatorial Designs with Selected Applications: Lecture Notes,'' Department of Combinatorics and Optimization, University of Waterloo, Waterloo, Ontario, December 1996.
[26] Tóth, G., ``A Note on Geometric Graphs,'' DIMACS Technical Report 99-17, 1999.
[27] Tóth, G., and Valtr, P., ``Geometric Graphs with Few Disjoint Edges,'' Discrete and Computational Geometry, 22, (1999), 633-642
[28] Valtr, P., ``Generalizations of Davenport-Schinzel Sequences,'' in R.L. Graham, J. Kratochvíl, J. Nesetril, and F.S. Roberts (eds.), Contemporary Trends in Discrete Mathematics, DIMACS Series, Vol. 49, American Mathematical Society, Providence, RI, 1999, 349-389.
[29] Valtr, P., ``Graph Drawings with no k Pairwise Crossing Edges,'' in G. DiBattista (ed.), Graph Drawing '97, Rome, 1997, 205-218.
[30] Valtr, P., ``On Geometric Graphs with no k Pairwise Parallel Edges,'' Discrete Comput. Geom., 19, (1998), 461-469.
[31] Winkler, P., ``Graph Homomorphisms and Long Range Order,'' DIMACS-DIMATIA Workshop on Graphs, Morphisms and Statistical Physics, DIMACS, March 2001.