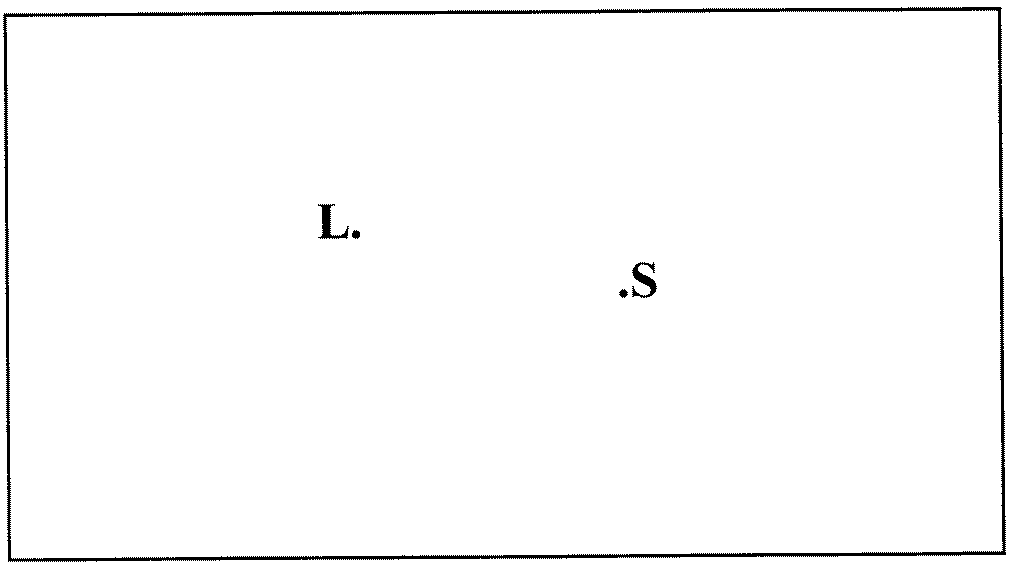
In Activity 3, you saw that it is possible to model a growth process in creating a Voronoi diagram, by using concentric circles and their intersections. In this activity, consider the territories created by male mouthbreeder fish (Tilapa mossambica) during the breeding season. On the sandy bottom, these fish "stake out" a spot for a breeding pit, then excavate the pit by spitting sand away from the center toward the pit centers of their neighbors, creating sand walls or "parapets" between the pits. Naturally the smaller the fish, the smaller his pit will be. (What does the box represent in this problem?)
In this activity, there are two sizes of fish, marked S(mall) and L(arge). On this scale representation of the sandy bottom, use the same process as for Activity 3 except that in this case, a small fish spits sand 0.5 inch per time period, while a large one spits it 1.0 inch. When you are finished finding the location of the parapets, you'll have the locations and sizes of the breeding pits for all the fish!
Caution: in this activity, it is not enough to find the intersection of just one pair of
circles, because the boundary between these pits is not the same as in the previous activities.
Suggestion: construct tiie circles in pairs, one from each site, increasing the radius after completing
each pair. When the pairs of circles intersect, carefully mark the point(s) of intersection before drawing
the next pair.
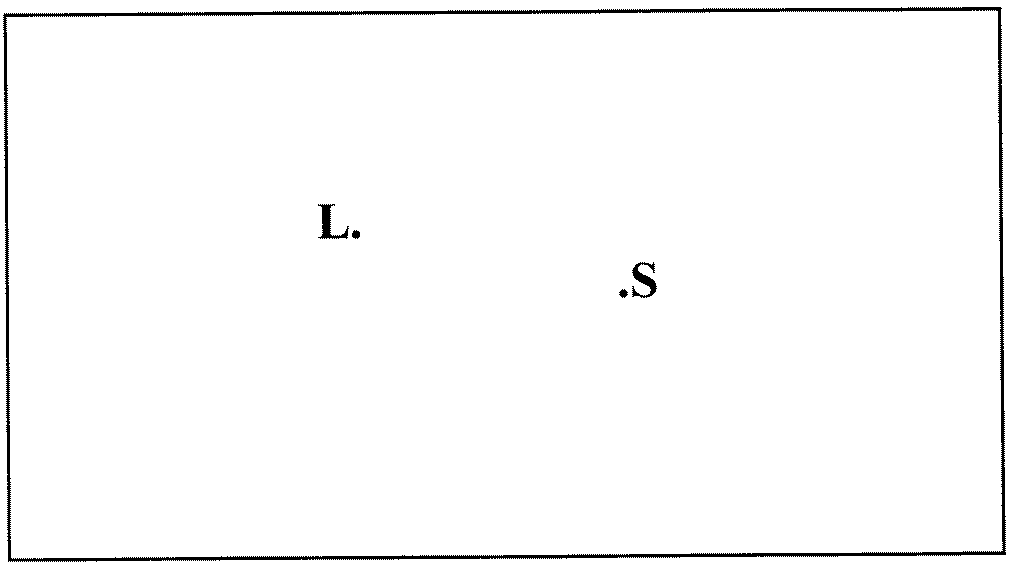
Writing assignment: Describe the shape of the boundary between these two breeding pits, and as much of the properties of this boundary as you can.