In Activity 1, you saw that you could define the service region for the restaurants by constructing the perpendicular bisector of the segment which connects them. Here's a slightly different problem setting:
Suppose that the three sites below represent the dens of three predatory animals in a certain region (the box again.) See if you can extend what you learned in Activity I to construct the boundaries between these dens which would define the "domains" or hunting regions for each of the animals. Assume that all of the animals have equal strength and influence, so that the perpendicular bisector of the segment between any two of them would define a boundary. Since this problem includes a third site, there is a portion of each perpendicular bisector that is closer to the third site than the two sites which determined that perpendicular bisector. Erase this part of the perpendicular bisector since it is not part of the boundary.
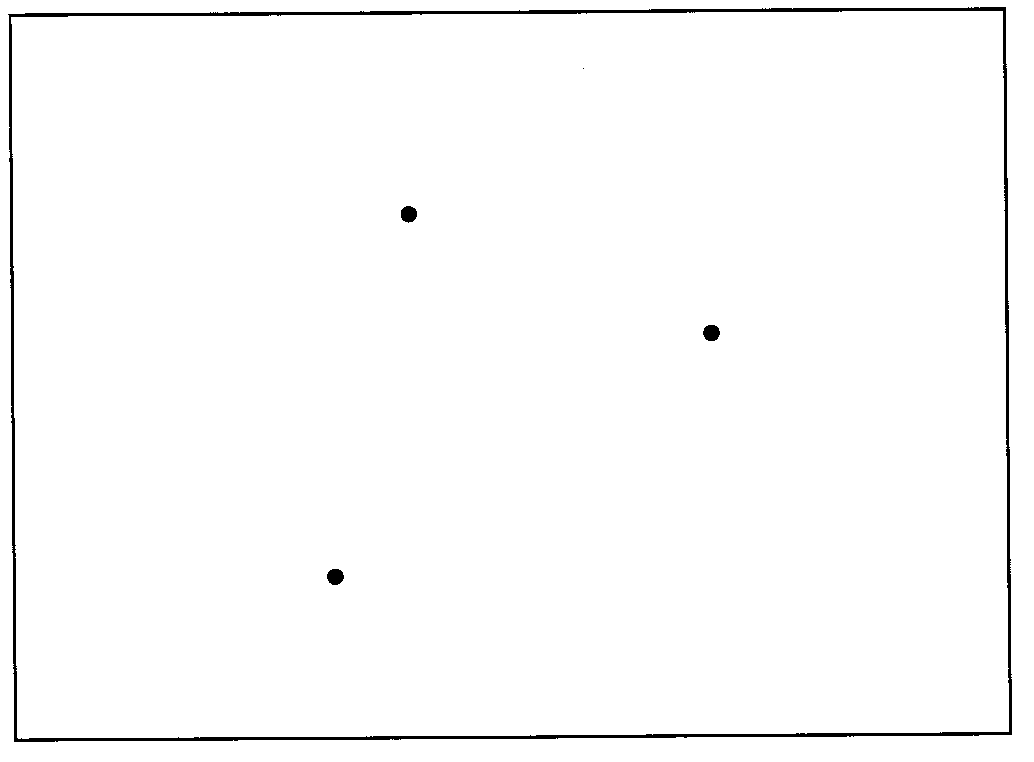
Writing assignment: How did you have to approach this problem differently from Activity 1, and how
was it the same? Notice that there is a point where all the boundaries intersect. What is the
significance of this point?